ISLR - Chapter 10. Deep Learning
- Chapter 10. Deep Learning
- 10.1. Single Layer Neural Networks
- 10.2. Multilayer Neural Networks
- 10.3. Convolutional Neural Networks
- 10.4. Document Classification
- 10.5. Recurrent Neural Networks
- 10.6. When to Use Deep Learning
- 10.7. Fitting a Neural Network
- 10.8. Interpolation and Double Descent
Chapter 10. Deep Learning
10.1. Single Layer Neural Networks
-
A neural network takes input vector of p variables \(X=(X_1,X_2,\ldots,X_p)\) and builds a nonlinear function $f(X)$ to predict the response Y. What distinguishes neural networks from these methods is the particular structure of the model.
-
E.g. a simple feed-forward neural network:
\(\begin{align*} f(X)&= \beta_0 + \sum_{k=1}^K\beta_k h_k(X) \\ &= \beta_0 + \sum_{k=1}^K\beta_k g(w_{k0}+\sum_{j=1}^p w_{kj}X_j). \end{align*}\)
In the terminology, the features \(X_1,\ldots,X_4\) make up the units in the input layer. Each of the inputs from the input lyaer feed into each of the K hidden units. In two steps; First the K activations $A_k$ in the hidden layer are computed as functions of the input features $X_1,\ldots,X_p$,
\(A_k = h_k(X) = g(w_{k0}+\sum_{j=1}^p w_{kj}X_j)\),
where \(g(z)\) is a nonlinear activation function that is specified in advance. We can think of each \(A_k\) as a different transformation \(h_k(X)\) of the original features, like basis functions of Chapter 7. These K activations then feed into the output layer, resulting in
\(f(X) = \beta_0 + \sum_{k=1}^K \beta_k A_k\),
a linear regression model. All the parameters $\beta_0,\ldots,\beta_K$ and $w_{10},\ldots,w_{Kp}$ need to be estimated from data. -
With deriving K new features by computing K different linear combinations of X, the model squashes each through an activation function $g(\cdot)$ to transform it. The final model is linear in these derived variables.
- Activation functions
- sigmoid activation function:
\(g(z)=\frac{e^z}{1+e^z}=\frac{1}{1+e^{-z}}\)
which is the same function used in logistic regression to convert a linear function into probabilities between zero and one. - ReLU(rectified linear unit) activation function:
\(g(z) = (z)_{+} = \begin{cases}0, & \mbox{if }z<0 \\ z, & \mbox{othersize}.\end{cases}\)
can be computed and stored more efficiently than a sigmoid function. Although it thresholds at zero, because we apply it to a linear function the constant term \(w_{k0}\) will shift this inflection point.
- sigmoid activation function:
-
The nonlinearity in the activation function \(g(\cdot)\) is essential, since without it the model would collapse into a simple linear model. Moreoever, having a nonlinear activation function allows the model to capture complex nonlinearities and interaction effects.
- Fitting a neural network requires estimating the unknown parameters. For a quantitative response, typically squared-error loss is used, so that the parameters are chosen to minimize \(\sum_{i=1}^n(y_i-f(x_i))^2\).
10.2. Multilayer Neural Networks
-
With H multiple hidden layers,
the first hidden layer is
\(\begin{align*} A_k^{(1)} &= h_k^{(1)}(X) \\ &= g(w_{k0}^{(1)}+\sum_{j=1}^p w_{kj}^{(1)}X_j) \end{align*}\)
for \(k=1,\ldots,K_1\).
The hth hidden layer treats the activations \(A_k^{(h-1)}\) as inputs and computes new activations
\(\begin{align*} A_{k'}^{(h)} &= h_{k'}^{(h)}(X) \\ &= g(w_{k'0}^{(h)}+\sum_{k'=1}^{K_1} w_{hk'}^{(h)}A_k^{(h-1)}) \end{align*}\)
for \(k'=1,\ldots,K_h\). Each \(A_{k'}^{(h)} = h_{k'}^{(h)}(X)\) is a function of input vector X. Thus, through a chain of transformations, the network is able to build up fairly complex transformations of X that ultimately feed into the output layer as features. -
The notation \(\mathbf{W}_h\) represents the entire matrix of weights that feed from the hidden layer $L_{h-1}$ to $L_h$. Each element $A_k^{(h-1)}$ feeds to the hidden layer $L_h$ via the matrix of weights \(\mathbf{W}_h\).
-
On the output layer in the classification case, compute M different linear models similar to our single model to get separate quantitative responses for each classes. To represent class probabilities \(f_m(X)=Pr(Y=m|X)\), we use the softmax activation function
\(f_m(X)=Pr(Y=m|X)=\frac{e^{Z_m}}{\sum_{l=0}^{M-1} e^{Z_l}}\).
The classifier assigns the image to the class with the highest probability. -
To train this network, since the response is qualitative, we look for coefficient estimates that minimize the negative multinomial log-likelihood
\(-\sum_{i=1}^n\sum_{m=0}^{M-1}y_{im}\log(f_m(x_i))\),
known as the cross-entropy, a generalization of the criterion for two-class logistic regression. If the response were quantitative, we would instead minimize squared-error loss as before.
10.3. Convolutional Neural Networks
10.3.1. Convolution Layers
-
A convolution layer is made up of a large number of convolution filters, each of which is a template that determines whether a particular local feature is present in an image. A very simple operation, called a convolution amounts to repeatedly multiplying matrix elements and then adding the results. Resulting convolved image highlights regions of the original image that resemble the convolution filter.
-
In a convolution layer, we use a whole bank of filters to pick out a variety of differently-oriented edges and shapes in the image. Using predefined filters in this way is standard practice in image processing. By contrast, we can think of the filter weights as the parameters going from an input layer to a hidden layer. Thus, with CNNs the filters are learned for the specific classification task.
10.3.2. Pooling Layers
- A pooling layer provides a way to condense a large image into a smaller summary image. The max pooling operation summarizes each non-overlapping block of pixels in an image using the maximum value in the block. This reduces the size of the image and also provides some location invariance.
10.3.3. Architecture of a Convolutional Neural Network
- Convolve-then-pool sequence:
Start with the three-dimensional feature map of a color image, consist of three $n\times n$ two-dimensional feature map of pixels.
Each convolve layer takes as input the three-dimensional feature map from the previous layer and treats it like a single multi-channel image. Each convolution filter learned has as many channels as this feature map.
Since the channel feature maps are reduced in size after each pool layer, we usually increase the number of filters in the next convolve layer to compensate.
Sometimes we repeat several convolve layers before a pool layer. This effectively increases the dimension of the filter.
These operations are repeated until the pooling has reduced each channel feature map down to just a few pixels in each dimension.
Then the three-dimensional feature maps are flattened; the pixels are treated as separate units, and fed into one or more fully-connected layers before reaching the output layer, which is a softmax activation for the classification.
10.3.4. Data Augmentation
-
Each training image is replicated many times, with each replicate randomly distorted in a natural way such that human recognition is unaffected. Typical distortions are zoom, horizontal and vertical shift, shear, small rotations, and horizontal flips. This is a way of increasing the training set considerably with somewhat different examples, and thus protects against overfitting.
-
We can see this as a form of regularization: we build a cloud of images around each original image, all with the same label. This kind of fattening of the data is similar in spirit to ridge regularization.
10.4. Document Classification
-
For the two-class response of the sentiment of the text data, which will be positive or negative. Each document can be a different length, include slang or non-words, have spelling errors, etc. We need to find a way to featurize such a document.
-
The simplest featurization is BOW, bog-of-words model. With dictionary containing M words, we create a binary feature vector of length M for each document, scoring 1 for presence, and 0 otherwise. The resulting training feature matrix X is a sparse matrix, most of the values are the same(to zero); it can be stored efficiently in sparse matrix format. Then we can build a neural network model with the feature matrix as input layers.
-
The bag-of-words model summarizes a document by the words present, and ignores their context. There are at least two popular ways to take the context into account:
- The bag-of-n-grams model recording the consecutive co-occurrence of every distinct set of words.
- Treat the document as a sequence, taking account of all the words in the context of those that preceded and those that follow.
10.5. Recurrent Neural Networks
-
In a recurrent neural network (RNN), the input object X is a sequence. Considering a corpus of documents, each document can be represented as a sequence of L words, so \(X=\left\{ X_1,X_2,\ldots,X_L\right\}\). RNNs are designed to capture the sequential nature of such(text) input objects like CNNs for the spatial structure of image inputs. The output Y can also be a sequence (such as in language translation), but often is a scalar, like the binary sentiment label of a movie review document.
-
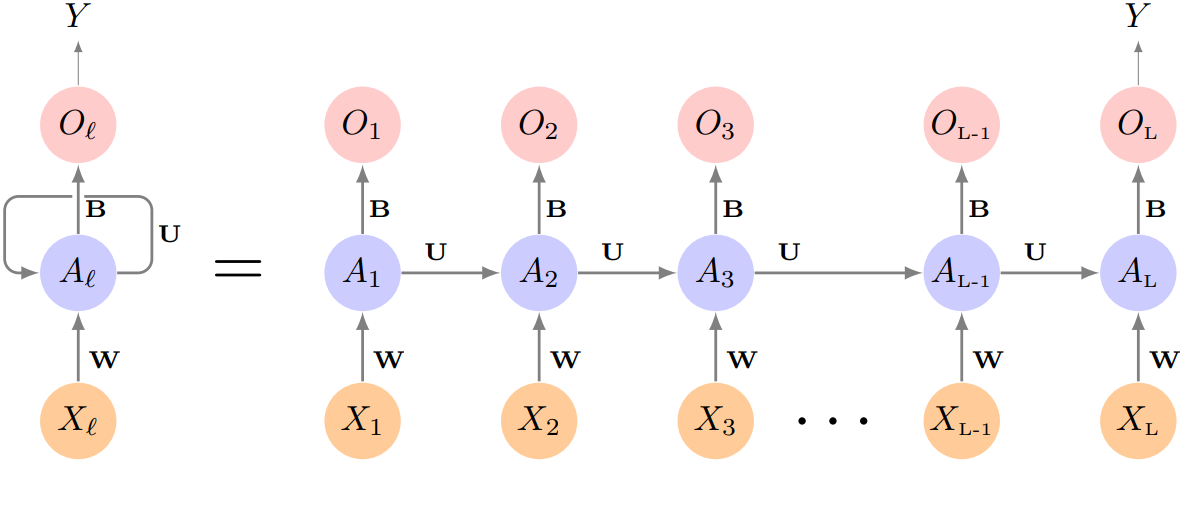
The structure of a very basic RNN; with a sequence \(X=\left\{ X_1,X_2,\ldots,X_L\right\}\), a simple output Y, and a hidden-layer sequence \(\left\{ A_l \right\}_1^L =\left\{ A_1,A_2,\ldots,A_L\right\}\). Each \(X_l\) is a vector representation for the $l$th word.
Suppose it has p components \(X_l^T = (X_{l1},X_{l2},\ldots,X_{lp})\), and hidden layer consists of K units \(A_l^T = (A_{l1},\ldots,A_{lK})\). We represent the collection of \(K \times (p+1)\) shared weights $w_{kj}$ for the input layer by a matrix W, and similarly U is a \(K \times K\) matrix of the weights $u_{ks}$ for the hidden-to hideen layers, and B is a K+1 vector of weights $\beta_k$ for the output layer.
Then \(A_{lk}=g(w_{k0}+\sum_{j=1}^p w_{kj}X_{lj} + \sum_{s=1}^K u_{ks} A_{l-1,s})\), and the output \(O_l = \beta_0 + \sum_{k=1}^K\beta_k A_{lk}\) for a quantitative response, for example. Here $g(\cdot)$ is an activation function such as ReLU. Note that the same weights W, U, and B are not functions of $l$. This is a form of weights sharing used by RNNs, similar to the use of filters in CNNs.
Proceeded from beginning to end, the activations $A_l$ accumulate a history of what has been seen before, so that the learned context can be used for prediction.
-
For regression problems the loss function is $(Y-O_L)^2$, which only references the final output \(O_L = \beta_0 + \sum_{k=1}^K\beta_k A_{Lk}\) and others before are not used. With n input sequence/response pairs, the parameters are found by minimizing the sum of squares \(\sum_{i=1}^n(y_i-o_{iL})^2\).
10.5.1. Sequential Models for Document Classification
-
Beacuse of the dimensionality problem of bag-of-words model(one-hot-encoded vector), we use lower-dimensional embedding space instead. Rather than representing each word by a binary vector with zeros and a single one in some position, we will represent it by a set of m real numbers, none of which are typically zero.
-
The embedding layer E comes from the optimization part of a neural network, or we can use a weight freezing, inserting a precomputed matrix E in the embedding layer. The idea is that the positions of words in the embedding space preserve semantic meaning: synonyms should appear near each other.
-
The next step is to limit each document to the last L words. Documents that are shorter get padded with zeros upfront. So now each document is represented by a series consisting of L vectors, and each $X_l$ in the sequence has m components.
-
Then we run the process of simple RNN as presented before, with B has 2(K+1) for two-class logistic regression. If the embedding layer E is learned, that adds an additional $m \times D$ parameters, and is by far the biggest cost.
-
More elaborate versions use long term and short term memory (LSTM). However, LSTM models take a long time to train, which makes exploring many architectures and parameter optimization tedious.
10.5.2. Time Series Forecasting
-
In an example of Stock price predition, one feature of stock market data is that the day-to-day observations are not independent of each other. The series exhibit auto-correlation; values nearby in time tend to be similar to each other.
-
Consider pairs of observations $(v_t,v_{t-l})$, a lag of $l$ days apart. If we take all such pairs in the $v_t$ series and compute their correlation coefficient, this gives the autocorrelation at lag $l$.
-
Another interesting characteristic of this forecasting problem is that the response variable $v_t$;
log_volumeis also a predictor. We will use the past values oflog_volumeto predict values in the future.
RNN forecaster
-
We wish to predict a value $v_t$ from past values $v_{t-1},v_{t-2},\ldots$ and also to make use of past values of the other series $r_{t-1},r_{t-2},\ldots$ and $z_{t-1},z_{t-2},\ldots$.
-
Idea: to extract many short mini-series of input sequences with a predefined length L(lag), and a corresponding target Y.
\(X_1= \begin{pmatrix} v_{t-L}\\ r_{t-L}\\ z_{t-L} \end{pmatrix}, X_2= \begin{pmatrix} v_{t-L+1}\\ r_{t-L+1}\\ z_{t-L+1} \end{pmatrix}, \cdots, X_L= \begin{pmatrix} v_{t-1}\\ r_{t-1}\\ z_{t-1} \end{pmatrix}\), and \(Y=v_t\).
Here the target Y is the value of response at a single timepoint t, and the input sequence X is the series of 3-vectors \(\left\{X_l\right\}_1^L\) consisting of measurements from day t-L, t-L+1, up to t-1. Each value of t makes a separate pair (X,Y). Then we run RNN model for prediction.
Autoregression
-
The RNN we just fit has much in common with a traditional autoregression(AR) linear model. Constructed a response vector y and a matrix M of predictors for least squares regression:
\(\mathbf{y}=\begin{bmatrix} v_{L+1}\\ v_{L+2}\\ \vdots\\ v_T \end{bmatrix}\), \(\mathbf{M}=\begin{bmatrix} 1 & v_L & v_{L-1} & \cdots & v_1 \\ 1 & v_{L+1} & v_{L} & \cdots & v_2 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & v_{T-1} & v_{T-2} & \cdots & v_{T-L} \end{bmatrix}\)
each have T-L rows, one per observation. The predictors for any given reponse $v_t$ on day t are the previous L values of the same series. Fitting a regression of y on M amounts to fitting the model
\(\hat{y}_t = \hat\beta_0 + \hat\beta_1 v_{t-1} + \hat\beta_2 v_{t-2} + \cdots + \hat\beta_L v_{t-L}\),
and is called an order-L autoregressive model, or simplay AR(L). - The RNN processes data sequence from left to right with the same weights W, while the AR model simply treats all L elements of the sequence equally as a vector of $L \times p$ predictors; a process called flattening in the neural network. Of course the RNN also includes the hidden layer activations which transfer information along the sequence, and introduces additional nonlinearity with much more parameters.
10.5.3. Summary of RNNs
- There are many variations and enhancements of the simple RNN for sequence modeling. One approach uses a onedimensional convolutional neural network, treating the sequence of vectors as an image. One can also have additional hidden layers; multi-layer RNN. Alternative bidirectional RNNs scan the sequences in both directions. In language translation the target is also a sequence of words, in a language different from that of the input sequence. Both the input sequence and the target sequence share the hidden units, so-called Seq2Seq learning.
10.6. When to Use Deep Learning
-
Should we discard all our older tools, and use deep learning on every problem with data? We follow Occam’s razor principle: when faced with several methods that give roughly equivalent performance, pick the simplest.
-
Typically we expect deep learning to be an attractive choice when the sample size of the training set is extremely large, and when interpretability of the model is not a high priority.
10.7. Fitting a Neural Network
-
In simple network, the parameters are \(\beta = (\beta_0,\beta_1,\ldots,\beta_K)\), each of the \(w_k=(w_{k0},w_{k1},\ldots,w_{kp})\) for k in K. Given observations ($x_i,y_i$) for i in n, we fit the model by solving a nonlinear least squares problem
\(\begin{align*}\text{min}_{\left\{ w_k \right\}_1^K, \beta }\frac{1}{2}\sum_{i=1}^n(y_i-f(x_i))^2,\end{align*}\)
where \(f(x_i)=\beta_0+\sum_{k=1}^K\beta_k g(w_{k0}+\sum_{j=1}^p w_{kj}x_{ij})\). -
The minimization objective is quite simple, but because of the nested arrangement of the parameters and the symmetry of the hidden units, it is not straightforward to minimize. The problem is nonconvex in the parameters, and hence there are multiple solutions. To overcome some of these issues and to protect from overfitting, two general strategies are employed when fitting neural networks: Slow learning and Regularization.
-
Suppose we represent all the parameters in one long vecter \(\theta\). Then we can rewrite the objective as
\(R(\theta)=\frac{1}{2}\sum_{i=1}^n(y_i-f_{\theta}(x_i))^2\), where we make explicit the dependence of f on the parameters. The idea of gradient descent is- Start with a guess \(\theta^0\) for all the parameters in \(\theta\), and set \(t=0\).
- Iterate until the objective fails to decrease:
(a) Find a vector \(\delta\) reflects a small change in \(\theta\), such that \(\theta^{t+1} = \theta^t + \delta\) reduces the objective; i.e. such that \(R(\theta^{t+1})<R(\theta^t)\).
(b) Set \(t \leftarrow t+1\).
10.7.1. Backpropagation
-
How do we find the directions to move \(\theta\) so as to decrease the objective? The gradient of $R(\theta)$, evaluated at some current value \(\theta=\theta^m\), is the vector of partial derivatives at that point:
\(\begin{align*}\triangledown R(\theta^m) = \frac{\partial R(\theta)}{\partial\theta}|_{\theta=\theta^m}\end{align*}\).
The subscript \(\theta=\theta^m\) means that after computing the vector of derivatives, we evaluate it at the current guess, \(\theta^m\). This gives the direction in $\theta$-space in which $R(\theta)$ increases most rapidly. The idea of gradient descent is to move $\theta$ a little in the opposite direction(since we wish to go downhill):
\(\theta^{m+1}\leftarrow\theta^m - \rho\triangledown R(\theta^m)\).
For a small enough value of the learning rate $\rho$, this step will decrease the objective $R(\theta)$; i.e. $R(\theta^{m+1})\le R(\theta^m)$. If the gradient vector is zero, then we may have arrived at a minimum of the objective. -
Calculation: the chain rule of differentiation
10.7.2. Regularization and Stochastic Gradient Descent
-
stochastic gradient descent(SGD):
When n is large, instead of calculating over all n observations, we can sample a small fraction or minibatch of them each time we compute a gradient step. -
Regularization:
E.g. Ridge regularization on the weights, augmenting the objective function with a penalty term on classification problem:
\(R(\theta;\lambda)=-\sum_{i=1}^n\sum_{m=0}^{M-1}y_{im}\log(f_m(x_i)) +\lambda\sum_j\theta_j^2\).
With $\lambda$ as preset at a small value or found using the validation-set approach. We can also use different values of $\lambda$ for the groups of weights from different layers. Lasso is also a popular alternative.
10.7.3. Dropout Learning
- Efficient form of regularization, similar in some respects to ridge regularization. The idea is to randomly remove a fraction of the units in a layer when fitting the model, separately each time a training observation is processed. This prevents nodes from becoming over-specialized, and can be seen as a form of regularization.
10.7.4. Network Tuning
- Choices that all have an effect on the performance:
The number of hidden layers, and the number of units per layer.
Regularization tuning parameters.
Details of stochastic gradient descent.
10.8. Interpolation and Double Descent
-
In certain specific settings it can be possible for a statistical learning method that interpolates the training data to perform well; or at least, better than a slightly less complex model that does not quite interpolate the data. The phenomenon is known as double descent, where the test error has a U-shape before the interpolation threshold is reached, and then it descends again (for a while, at least) as an increasingly flexible model is fit. The double-descent phenomenon does not contradict the bias-variance trade-off.
-
It has been used by the machine learning community to explain the successful practice of using an overparametrized neural network (many layers, and many hidden units), and then fitting all the way to zero training error. However, zero error fit is not always optimal, we typically do not want to rely on this behavior.