ISLR - Chapter 4. Classification
- Chapter 4. Classification
- 4.1. Overview of Classification
- 4.2. Why Not Linear Regression?
- 4.3. Logistic Regression
- 4.4. Generative Models for Classification
- 4.5. A Comparison of Classification Methods
- 4.6. Generalized Linear Models
2020-04-15
Chapter 4. Classification
4.1. Overview of Classification
- Response Y is qualitative(categorical) variable.
Predicting a qualitative response, classification
4.2. Why Not Linear Regression?
- Problem of linear regression in classification
e.g. in binary response group: Y = 0 or 1
Model prediction: $\hat y_i = x_i^T \hat\beta$; $\quad$ where $\beta$ is LSE
Decision rule: if $ \hat y_i > 0.5 $, classify ith obs. to group 1
BUT, possible value of estimates outside the interval,
$ \hat Y >1 \text{ or } \hat Y <0 $: do not fit for the range of Y
4.3. Logistic Regression
4.3.1. The Logistic Model
-
Supoose that Y has 2 classes where
$p(X)=P(Y=1|X)$, $X=(1,X_1, \ldots, X_p)^T$, $\beta=(\beta_0,\beta_1,\ldots, \beta_p)^T$ -
\(p(X)= \frac{e^{x^T\beta}}{1+e^{x^T\beta}}\): logistic function
\(0 < \frac{p(X)}{1-p(X)} = e^{x^T\beta} < \infty\): odds relative to range of $p(X)= [0,1]$
\(\log\frac{p(X)}{1-p(X)} = X^T \beta\): log odds or logit
4.3.2. Estimating the Regression Coefficients: MLE
-
as $\log\frac{p(X)}{1-p(X)} = X^T \beta $, $ p(X) = \frac{e^{x^T\beta}}{1+e^{x^T\beta}} $, $ e^{x^T\beta} = \frac{p(X)}{1-p(X)}$
where $Y_i | X_i \sim$ Bernoulli($p(X_i)$),
$\rightarrow \prod_{i=1}^N p(x_i)^{y_i} (1-p(x_i))^{1-y_i}$
likelihood function L = $\prod_{i:y_i=1}p(x_i) \prod_{i:y_i=0}(1-p(x_i))$ -
Maximum Likelihood Estimation MLE:
\(\hat\beta = \text{max}_\beta [\prod_{i:y_i=1} \frac{e^{x^T\beta}}{1+e^{x^T\beta}} \prod_{i:y_i=0} \frac{1}{1+e^{x^T\beta}}]\)
take log and get log-likelihood function $l(\beta)$ and least squares $\hat\beta$ -
But we cannot find analytic solution for $\frac{\partial l(\beta)}{\partial\beta} = 0$,
use Newton-Raphson method, a numerical method to find $\hat\beta$. -
if $\hat\beta >0$ , p(X) increases by a unit change in X
if $\hat\beta <0$ , p(X) decreases by a unit change in X
(not a linear relationship, but a direction)
4.3.3. Multinomial Logistic Regression
-
$P(Y=k | X=x) = \frac{e^{x^T\beta_k}}{1+\sum_{j=1}^{K-1} e^{x^T\beta_j}}$
$P(Y=K | X=x)= \frac 1{1+\sum_{j=1}^{K-1} e^{x^T\beta_j}}$ -
$\log\frac{P(Y=k | X=x)}{P(Y=K | X=x)} = x^T\beta_k $
for $ k=1,\cdots, K-1$ with $\sum_{k=1}^K P(Y=k | X=x) = 1 $
the choice of denominator the $K_{th}$ class is arbitary -
ML estimation (by numerical method):
we can have K-1 equations and K-1 number of $\hat\beta_k$ (MLE)
4.4. Generative Models for Classification
-
By logistic regression directly modeling $Pr(Y=K | X=x)$,
in statistical jargon, we model the conditional distribution
of the response Y, given the predictor(s) X. - then Why do we need another method?
- when there is substantial separation between 2 classes and logistic model’s parameter estimates are unstable
- when X approximately follow normal distribution and the sample size is small
- in the case of more than two response classes
-
In Generative approach, we model the distribution of the predictors X separately to the response class then use Bayes’ theorem to get $Pr(Y=K | X=x)$.
if X for each Ys assumed to follow the normal distribution,
model has very similar form to logistic regression. -
Suppose that we classify an obs. into one of K$\ge 2 $ classes
$f_k(x)$; is the density funtion of X in class k,
$\pi_k$; is the prior probability of class k with $\sum_{k=1}^K \pi_k =1$ - Bayes’ Theorem
$ Pr(Y=k | X=x) = \frac{\pi_k f_k(x)}{\sum_{l=1}^K \pi_l f_l(x)}$
$ Pr(Y=k | X=x) $ is the posterior probability of obs. at x belongs to k
4.4.1. LDA: Linear Discriminant Analysis for $p = 1$
- Assumptions:
a Gaussian or normal distribution $f_k(x)$- $f_k(x) = \frac{1}{\sqrt{2\pi}\sigma_k}exp\left(-\frac{1}{2\sigma_k^2}(x-\mu_k)^2\right)$
- $\mu_k$ is the mean for the kth class
- $\sigma_k^2$ is the shared variance across for all K classes(=$\sigma^2$)
- $p_k(x) = \frac{\pi_k \frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{1}{2\sigma^2}(x-\mu_k)^2\right)} {\sum_{l=1}^K \pi_l \frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{1}{2\sigma^2}(x-\mu_l)^2\right)}$
-
Bayes Classifier assigns an observation X = x to the class
having lagest value of: \(\delta_k(x) = x\cdot\frac{\mu_k}{\sigma^2} - \frac{\mu_k^2}{2\sigma^2} + \log(\pi_k)\) -
But in real-life situation,
such assumptions are not enough to apply the Bayes classifier.
have to estimate the parameters $\mu_1,\ldots,\mu_K,\ \pi_1,\ldots,\pi_K$ and $\sigma^2$
$\rightarrow$ LDA method used to approximate the Bayes classifier. -
LDA estimates model parameters:
$\hat\pi_k = n_k/n$
$\hat\mu_k = \sum_{i:y_i=k}x_i / n_k $
\(\begin{align*}\hat\sigma_k^2 = \sum_{k=1}^K\sum_{i:y_i=k}(x_i-\hat\mu_k) / (n-K) \end{align*}\) - LDA classifier assigns an observation X = x to the class
having lagest value of discriminant function: \(\hat\delta_k(x) = x\cdot\frac{\hat\mu_k}{\hat\sigma^2} - \frac{\hat\mu_k^2}{2\hat\sigma^2} + \log(\hat\pi_k)\)
4.4.2. LDA: Linear Discriminant Analysis for $p > 1$
- Assumptions:
X from a multivariate Gaussian(or multivariate normal) distribution,
where each individual predictor follows a one-dimensional normal distribution,
with a class-specific mean vector and a common covariance matrix- $f_k(x) ~ \text{MVN}(\mu_k,\Sigma_k)$
- $\mu_k$ is a $p \times 1$ vector, the mean for the kth class
- $\Sigma_k = \Sigma$ is a $p \times p$ covariance matrix for all K classes
-
Find k maximizing \(\log P(Y=k|X=x)\):
\(\begin{align*} \log P(Y=k|X=x) &= \log\frac{f_k(x)\pi_k}{\sum_{j=1}^K f_j(x)\pi_j}\\ &= \log(f_k(x)\pi_k) + C_1 \\ &= \cdots \\ &= \log\pi_k - \frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k + x^T\Sigma^{-1}\mu_k + C_3\\ &= \delta_k(x) + C_3 \cdots \scriptstyle\text{ : Linear discriminant function (linear in X)} \\ \Rightarrow \hat Y &= \text{argmax}_k \delta_k(x) \end{align*}\) -
Decision boundary is also in a linear form.
when solving x: $\delta_k(x) = \delta_l(x)$, we can have linear form of decision boundary. -
LDA estimates model parameters:
$\hat\pi_k = n_k/n$
$\hat\mu_k = \sum_{i:y_i=k}x_i / n_k $
\(\begin{align*}\hat\Sigma_k = \sum_{k=1}^K\sum_{y_i=k}(x_i-\hat\mu_k)(x_i-\hat\mu_k)^T / (n-K) \end{align*}\) -
ROC curve, receiver operating characteristics
to display two types of errors for all possible thresholds
useful for comparing different classifiers
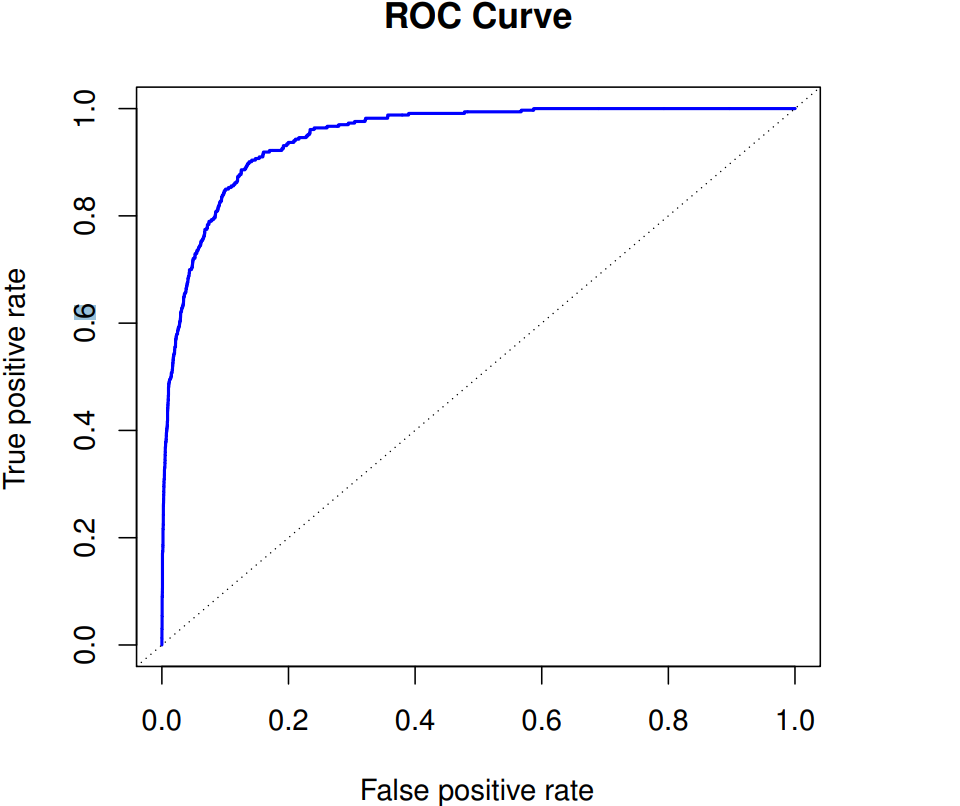
-
AUC, area under the (ROC) curve
overall performance of a classifier summarized over all possible thresholds - sensitivity and specificity, from confusion matrix
changes of true positive and false positive rate by varying the classifier threshold


4.4.3. QDA: Quadratic Discriminant Analysis
-
Assumption: Same as LDA, but “$\Sigma_k \ne \Sigma$” for all K classes
-
Quadratic discriminant function:
$\delta_k(x)= \log\pi_k - \frac{1}{2}\log| \Sigma_k | - \frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k) $ -
Decision boundary is in quadratic line.
-
Estimation of parameters:
$\hat\pi_k = n_k/n$
$\hat\mu_k = \sum_{y_i=k}x_i / n_k $
\(\begin{align*}\hat\Sigma_k =\sum_{y_i=k}(x_i-\hat\mu_k)(x_i-\hat\mu_k)^T / (n-1) \end{align*}\) (only obs. in $k_{th}$ group) - LDA vs. QDA: the bias-variance trade-off
- LDA
for p predictors, covariance matrix requires estimating $p(p+1)/2$ parameters.
linear model in x, which means there are $Kp$ linear coefficients
less flexible classifier having lower variance and potential of improved prediction performance
but with assumption of shared variance, LDA can suffer from high bias
when there are relatively few training observations and reducing variance is crucial - QDA
for p predictors, estimating seperate covariance matrix requires estimating $Kp(p+1)/2$ parameters.
when there are very large training set, the variance of the classifier is not a major concern
or there is no common covariance matrix for the K classes
- LDA
- LDA vs. Logistic Regression
- LDA:
MVN assumption needed
Qualitative(categorical) inputs are not available - Logistic:
No assumption needed and Y ~ Bernoulli is evident; $\rightarrow$ robust model
Qualitative are available
can run F-test to choose more important features
- LDA:
4.4.4. Naive Bayes
-
Bayes’ theorem expands posterior prob. $p_k(x) = Pr(Y=k|X=x)$ with two terms:
$\pi_k$ is a prior prob. that an observation belongs to kth class
$f_k(x)$ is a p-dim. density function for an observation in the kth class -
Estimations:
$\hat\pi_k$ as the proportion of training observations belonging to the kth class.
$\hat{f}_k(x)$ is more challenging, as we must consider both marginal and joint distribution of predictors, in a multivariate normal distribution, the joint distribution is summarized by the off-diagonal elements of the covariance matrix, but this association is still hard to be characterized. - to simplifies task:
- LDA assumes,
MVN distribution $f_k(x)$ with class-specific mean and shared variance - QDA assumes,
MVN distribution $f_k(x)$ with class-specific mean and class-specific variance - naive Bayes assumes,
Within the $k$th class, the $p$ predictors are independent, or,
$f_k(x) = f_{k1}(x_1) \times f_{k2}(x_2) \times \cdots \times f_{kp}(x_p)$ where
$f_{kj}$ is the density function of the jth predictor among observations in the kth class.
a simple assumption that there is NO association between the predictors
- LDA assumes,
-
the posterior probability $p_k(x)$
$Pr(Y=k|X=x) = \frac{\pi_k\times f_{k1}(x_1)\times f_{k2}(x_2)\times\cdots\times f_{kp}(x_p)} {\sum_{l=1}^K\pi_l}\times f_{l1}(x_1)\times f_{l2}(x_2)\times\cdots\times f_{lp}(x_p)$ - To estimate the one-dimensional density function $f_{kj}$:
- for quantitative $X_j$, we can assume that $X_j|Y = k \sim N(\mu_{jk}, \sigma_{jk}^2)$ within each class, the jth predictor $X_j$ is drawn from a normal distribution
- for quantitative $X_j$, or, we use a non-parametric estimate for $f_{kj}$ estimate $f_{kj}(x_j)$ as the fraction of the training observations in the kth class that belong to the same histogram bin as $x_j$, or we can use a kernel density estimator instead of histogram
- for qualitative $X_j$, we can simply count the proportion of training observations for the jth predictor corresponding to each class.
4.5. A Comparison of Classification Methods
4.5.1. An Analytical Comparison
- analytical (or mathematical) comparison of LDA, QDA, naive Bayes, and logistic regression
in a setting K as the baseline class and classify to the class that maximizes
\(log\left(\frac{Pr(Y=k|X=x)}{Pr(Y=K|X=x)}\right)\)- LDA:
\(\begin{align*} \log\left(\frac{Pr(Y=k|X=x)}{Pr(Y=K|X=x)}\right) &= \log\left(\frac{\pi_k f_k(x)}{\pi_K f_K(x)}\right) \\ &= \log\left(\frac{\pi_k exp(-\frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k))} {\pi_K exp(-\frac{1}{2}(x-\mu_K)^T\Sigma^{-1}(x-\mu_K))}\right) \\ &= \log\left(\frac{\pi_k}{\pi_K}\right) - \frac{1}{2}(\mu_k+\mu_K)^T\Sigma^{-1}(\mu_k-\mu_K) \\ &\quad + x^T\Sigma^(\mu_k-\mu_K)\\ &= a_k + \sum_{j=1}^p b_{kj}x_j, \end{align*}\)
where $b_jk$ is the jth component of $\Sigma^{-1}(\mu_k-\mu_K)$ - QDA:
\(\log\left(\frac{Pr(Y=k|X=x)}{Pr(Y=K|X=x)}\right) = a_k + \sum_{j=1}^p b_{kj}x_j + \sum_{j=1}^p\sum_{l=1}^p c_{kjl}x_j x_l\) - naive Bayes:
\(\begin{align*} \log\left(\frac{Pr(Y=k|X=x)}{Pr(Y=K|X=x)}\right) &= \log\left(\frac{\pi_k f_k(x)}{\pi_K f_K(x)}\right) \\ &= \log\left(\frac{\pi_k\prod_{j=1}^p f_{kj}(x_j)} {\pi_K\prod_{j=1}^p f_{Kj}(x_j)}\right) \\ &= \log\left(\frac{\pi_k}{\pi_K}\right) + \sum_{j=1}^p\log\left(\frac{f_{kj}(x_j)}{f_{Kj}(x_j)}\right) \\ &= a_k + \sum_{j=1}^p g_{kj}(x_j) \end{align*}\)
which takes the form of a generalized additive model - Logistic Regression:
\(\log\left(\frac{Pr(Y=k|X=x)}{Pr(Y=K|X=x)}\right) = \beta_{k0} + \sum_{j=1}^p\beta_{kj}x_j\)
- LDA:
- LDA is a special case of QDA with $c_{kjl}=0$ and including any classifier
with linear decision boundary, is also a special case of naive Bayes with
$g_{kj}(x_j) = b_{kj}(x_j)$,
if in the naive Bayes classifier, we model $f_{kj}(x_j)$ using a one-dimensional Gaussian distribution $N(\mu_{kj},\sigma_j^2)$, we get $g_{kj}(x_j) = b_{kj}(x_j)$ where $b_{kj} = (\mu_{kj}-\mu_{Kj})/{\sigma_j^2}$. Then naive Bayes is a special case of LDA with variance restriced to be a diagonal matrix with jth diagonal element equal to $\sigma_j^2$. - Neither QDA nor naive Bayes is a special case of the other.
Navie Bayes is in a additive fit, a function of $x_j$ can be added but never multipied. By contrast, QDA takes terms of $c_{kjl}x_j x_l$. - both LDA and Logistic are linear function of the predictors. Predictors in LDA follow a normal distribution, while the coefficients in Logistic are chosen to maximize the likelihood function. LDA outperforms when the normality assumption holds and vice versa for Logistic.
- KNN outperforms LDA and Logistic when the decision boundary is highly non-linear provided with large n obs. to small p. KNN tends to reduce bias while incurring a lot of variance.
- QDA may be preferrend to KNN when decision boundary is non-linear but n is only modest, or p is not very small. Taking a parametric form, it requires a smaller sample size for accurate classification relative to KNN.
4.5.2. An Empirical Comparison
-
empirical (practical) comparison of classification performances,
we can draw boxplots of test error rates. -
shortly, no one method will dominate the others in every situation.
LDA and Logistic will tend to perform well when decision boundaries are linear. QDA or naive Bayes may be better in non-linear decision boundaries. KNN, non-parametric one is good for much more complicated decision boundaries. -
Like in regression using transformations of the predictors, including powers of predictors, we could create a more flexible logistic regression or LDA model. Adding quadratic terms and cross-products to LDA, we can have a model at somewhere between an LDA and a QDA.
4.6. Generalized Linear Models
- when Y is neither qualitative nor quantitative;
a discrete variable Y takes on non-negative integer values, or counts
and treat predictors X as qualitative variables.
4.6.1. Linear Regression Problems
- a linear regression model seems to provide reasonable and intuitive results on
those Y, for example, compared to the clear weather as baseline, there should be
negative coefficients to predict bike users on cloudy days and some lower values
on rainy days.
but there are some problems left in a linear model.
-
Negative fitted values relative to non-negative response Y. It raise concerns about the accuracy of model; coefficient estimates, confidence intervals, and other outputs
-
Mean-variance violates the assumptions of linear model. We assumed error term $\epsilon$ to have zero mean and constant value of variance $\sigma^2$, but in practice, the variance of $Y_i$ has some definite relationship to the expectation of $Y_i$. This problem is from the heteroscedasticity of the data.
- A solution: transformed response $\log(Y) = \sum_{j=1}^p X_j\beta_j + \epsilon $
It can avoids the possibility of negative predictions and overcomes much of the heteroscedasticity. But there may be a challenge in interpretation and in the fact that log transformation cannot be applied to the responses with the value of zero.
Thus, we introduce a Poisson Regression.
4.6.2. Poisson Regression
-
For a random variable Y takes on nonnegative integer values,
introduces $\lambda>0, \lambda = E(Y) = Var(Y)$;
Poisson distribution $Pr(Y=k) = \frac{e^{-\lambda}\lambda^k}{k!}$ -
a function of $ E(Y) = \lambda $ of the covariates $X_j$:
$\log(\lambda(X_1,\ldots,X_p)) = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p$ or
$\lambda(X_1,\ldots,X_p) = e^{\beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p}$
predicting mean value of Y in particular conditions(values) of predictor $X_j$s -
likelihood $l(\beta_0,\beta_1,\ldots,\beta_p) = \prod_{i=1}^n\frac{e^{-\lambda(x_i)}\lambda(x_i)^{y_i}}{y_i !}$
where $\lambda(x_i) = e^{\beta_0 + \beta_1 x_{i1} + \ldots + \beta_p x_{ip}}$
By solving MLE in this likelihood function, we can have similar fit to the response,
while we have more statistical significance of coefficients. -
Some important distinctions from the linear regression model.
- Interpretation: a one-unit change in $X_j$ is associated with the change by a factor of $ exp(\beta_j) $, or $ e^{\beta_j} $ in E(Y) = $\lambda$.
- Mean-variance relationship: under the introduced term $\lambda = E(Y) = Var(Y)$, the Poisson model is more adequate to the data with heteroscedasticity.
- No nonnegative fitted values
4.6.3. Generalized Linear Models in Greater Generality
- Common characteristics of Linear, Logistic, Poisson Regressions:
- Use p predictors $X_j$ to predict a response Y and assume that conditional $P(Y|X)$
belongs to a certain family of distributions(Gaussian, Bernoulli, Poisson distribution).
$*$which are in exponential family(with exponential, Gamma, negative binomial distributions) - Modeling the mean of Y, or expected, $E(Y)$ as a function of predictors X.
$\text{in Linear: } E(Y|X_1,\ldots,X_p) = \beta_0 + \beta_1 X_1, + \cdots + \beta_p X_p$
\(\begin{align*} \text{in Logistic: } E(Y|X_1,\ldots,X_p) &= Pr(Y=1|X_1,\ldots,X_p) \\ &= \frac{e^{\beta_0 + \beta_1 X_1, + \cdots + \beta_p X_p}} {1+e^{\beta_0 + \beta_1 X_1, + \cdots + \beta_p X_p}} \end{align*}\)
\(\begin{align*} \text{in Poisson: } E(Y|X_1,\ldots,X_p) &= \lambda(X_1,\ldots,X_p) \\ &= e^{\beta_0 + \beta_1 X_1, + \cdots + \beta_p X_p} \end{align*}\)
which can be expressed using a link function, $\eta$, applying a transformation that $\eta(E(Y|X_1,\ldots,X_p)) = \beta_0 + \beta_1 X_1, + \cdots + \beta_p X_p$
and each $\eta(\mu)$ is $\mu, \log(\mu/(1-\mu)), \log(\mu)$; respectively to models.
- Use p predictors $X_j$ to predict a response Y and assume that conditional $P(Y|X)$
belongs to a certain family of distributions(Gaussian, Bernoulli, Poisson distribution).
- GLM, a general recipe of regression approach:
with the response Y from one of the exponential family, transform expected Y(or mean) as a linear function of the predictors, we can have a regression model.