ISLR - Chapter 6. Linear Model Selection and Regularization
- Chapter 6. Linear Model Selection and Regularization
- 6.1. Subset Selection
- 6.2. Shrinkage Methods
- 6.3. Dimension Reduction Methods
- 6.4. Considerations in High Dimensions
Chapter 6. Linear Model Selection and Regularization
- Limitations of LSE
- Prediction Accuracy:
- if n is not much larger than p, the least squares fit can have a lot of variability, results in overfitting and poor predictions to test data.
- if p > n, there is no unique solution for the least squares coefficient estimate; as $ Var(\hat\beta)=\infty$.
- if p is large, there can be correlations between X variables. A model
having multicollinearity can have high variance.
Constraining or Shrinking the estimated coefficients can reduce the variance with negligible increase in bias, and improve in the accuracy to the test data.
- Model Interpretability:
- There are irrelevant variables $X_j$. Removing by setting coefficient estimates
$\beta_j = 0$, we can have more interpretability.
Feature selection or Variable selection can exclude irrelevant variables from a multiple regression model.
- There are irrelevant variables $X_j$. Removing by setting coefficient estimates
$\beta_j = 0$, we can have more interpretability.
- Prediction Accuracy:
6.1. Subset Selection
6.1.1. Best Subset Selection
-
fit a separate least squares regression for all $2^p$ possible models with combinations of the p predictors.
- Algorithm
- $\mathcal{M}_0$ as null model (i.e., $ Y = \beta_0 + \epsilon $)
- For $ k = 1, 2, \ldots, p $:
(a) Fit all \({p \choose k}\) models with k predictors
(b) Pick the smallest RSS, (or largest $R^2$) = $ \mathcal{M}_k $ - Select best model among $\mathcal{M}_0, \ldots,\mathcal{M}_p$ using cross-validated prediction error, $C_p$ (AIC), BIC, or adjusted $R^2$
-
Guarantees the best selection, while it suffers from computational limitations. Also, it only works for least squares linear regression.
- in the case of logistic regression, we use deviance, $-2\log$MLE, instead of RSS in the 2nd step of algorithm upon.
6.1.2. Stepwise Selection
Forward Stepwise Selection
- Algorithm
- $\mathcal{M}_0$ as null model
- For $ k = 1, 2, \ldots, p $:
(a) Fit all p - k models in \(\mathcal{M}_k\) with one additional predictor
(b) Pick the smallest RSS among p - k models, $\mathcal{M}_{k+1}$ - Select best model among $\mathcal{M}_0, \ldots,\mathcal{M}_p$ with CV scores
- Total $\frac{p(p+1)}{2}+1$ possible models. No guarantee but available for the case of high dimensional data($n<p$).
Backward Stepwise Selection
- Algorithm
- $\mathcal{M}_p$ as full model, contains all p predictors
- For $ k = p, p-1, \ldots, 1 $:
(a) Fit all k - 1 models contain all but one of the predictors in \(\mathcal{M}_k\)
(b) Pick the smallest RSS among k - 1 models, $\mathcal{M}_{k-1}$ - Select best model among $\mathcal{M}_0, ldots,\mathcal{M}_p$ with CV scores
- Total $\frac{p(p+1)}{2}+1$ possible models. No guarantee and not for n < p case.
Hybrid Approaches
- add then remove one predictors in each step.
6.1.3. Choosing the Optimal Model
- A model containing all of the predictors will always have the smallest RSS and the largest $R^2$, since these quantities are related to the training error. Instead, we need a model with a low test error.
-
$C_p = \frac{1}{n}(RSS + 2 d \hat\sigma^2)$
For a fitted least squares model, with d as the number of predictors and $\hat\sigma^2$ as an estimate of the variance of the error. Typically $\hat\sigma^2$ is estimated using the full model containing all predictors. Adding a penalty to the training RSS is to adjust its underestimation to the test error. As the number of predictors increase, the penalty increase. If there is a proof of $\hat\sigma^2$ is an unbiased estimate of $\sigma^2$, $C_p$ is an unbiased estimate of test MSE. Then, a model with the lowest $C_p$ is the best model. -
AIC $= \frac{1}{n}(RSS + 2 d \hat\sigma^2)$
For a models fit by maximum likelihood(MLE), given by omitted irrelevant constants. $C_p$ and AIC are proportional to each other. -
BIC $= \frac{1}{n}(RSS + \log(n)d\hat\sigma^2)$
From a Bayesian point of view, for a fitted least squares model. Also given by omitted irrelevant constants. BIC has heavier penalty then $C_p$ or AIC, results in selecting smaller models. -
Adjusted $R^2 = 1 - \frac{RSS/(n-d-1)}{TSS/(n-1)}$
Since the usual $R^2$ is defined as $1 - RSS/TSS$, it always increases as more variables added. Adjusted $R^2$ gives penalty of d, the number of predictors in the denominator. Unlike other statistics, a large value of adjusted $R^2$ indicates a small test error.
Validation and Cross-Validation
- one-standard-error rule
First calculate the standard error of the estimated test MSE for each model size, then select the smallest model for which the estimated test error is within one standard error of the lowest point on the curve.
If a set of models appear to be more or less equally good, then we might as well choose the simplest model; the model with the smallest number of predictors.
6.2. Shrinkage Methods
6.2.1. Ridge Regression
-
Ridge regression coefficient estimates
\(\begin{align*} \hat\beta^R &= \text{min}_{\beta}\left[ \underbrace{\sum_{i=1}^n(y_i-\beta_0-\sum_{j=1}^p \beta_j x_{ij})}_{RSS} + \lambda\sum_{j=1}^p \beta_j^2 \right] \\ &= (X^TX + \lambda I)^{-1} X^T\underline{y} \end{align*}\) -
$\lambda \ge 0 $ is a tuning parameter, $\lambda\sum_{j=1}^p \beta_j^2$ is a shrinkage penalty. The penalty is small when the coefficients are close to zero, and so it has the effect of shrinking the estimates of $\beta_j$ towards zero. Ridge regression will produce a different set of coefficient estimates $\beta_{\lambda}^R$, for each value of $\lambda$.
-
We do not want to shrink the intercept $\beta_0$, which is simply a measure of the mean value of the response when $x_{i1}=x_{i2}=\ldots=x_{ip}=0$. If the variables, the columns of the data matrix $X$, have been centered to have mean zero before ridge regression is performed, then the estiamted intercept will take the form $\hat\beta_0 = \bar{y} = \sum_{i=1}^n y_i/n$.
-
The standard least squares coefficient estimates are scale equivariant; multiplying $X_j$ by a constant c leads to a scaling of the least squares coefficient estimates by a factor of 1/c. I.e., regardless of how the jth predictor is scaled, $X_j\hat\beta_j$ will remain the same.
In contrast, the ridge regression coefficient estimates can change substantially when multiplying a given predictor by a constant. The value of $X_j\hat\beta_{j,\lambda}^R$ may depend on the scaling of the other predictors. Thus, before applying ridge regression, the variables need to be standardized to have a standard deviation of one.
The formula: \(\tilde{x}_{ij}=\frac{x_{ij}}{\sqrt{\frac{1}{n}\sum_{i=1}^n(x_{ij}-\bar{x}_j)^2}}\) -
Ridge regression overperforms the standard least squares when the number of variables p is almost as large as the number of observations n, or even when $p > n$. Also it has computational advantages over best subset selection, which requires searching through $2^p$ models. Ridge regression only fits a single model for any fixed value of $\lambda$.
in Singular Value Decomposition
- where $ X = \mathbb{UDV}^T$,
\(\begin{align*} X\hat\beta^{\text{LSE}} &= X(X^TX)^{-1}X^T\underline{y} \\ &= \mathbb{UU}^T\underline{y} \\ X\hat\beta^R &= UD(D^2 + \lambda I)^{-1}DU^T\underline{y} \\ &= \sum_{j=1}^p\underline{u}_j\frac{d_{ij}^2}{d_{ij}^2+\lambda}\underline{u}_j^T\underline{y} \end{align*}\)
\(\begin{align*} \rightarrow \partial f(\lambda) &= tr[X(X^TX + \lambda I)^{-1} X^T] \\ &= tr(\mathbb{H}_{\lambda}) \\ &= \sum_{j=1}^p\frac{d_{ij}^2}{d_{ij}^2+\lambda} \end{align*}\)
6.2.2. The Lasso
-
Ridge regression estimates shrink towards zero but will not set nay of them exactly to zero(unless $\lambda = \infty$). This may not be a problem for prediction accuracy, but it can be a challenge in model interpretation when p is quite large.
-
The lasso
\(\hat\beta^L_{\lambda} = \text{min}_{\beta}\left[RSS+\lambda\sum_{j=1}^p|\beta_j|\right]\)
Instead of $\mathcal{l}_2$ penalty in Ridge, the lasso uses an $\mathcal{l}_1$ penalty. The $\mathcal{l}_1$ norm of a coefficient vector $\beta$ is given by $\lVert \beta \rVert_1 = \sum |\beta_j|$. This penalty has the effect of forcing some of the coefficient estimates to be exactly equal to zero when the tuning parameter is sufficiently large. Hence, the lasso performs variable selection, these sparse models with the lasso are much easier to interpret than those with ridge.
Another Formulation for Ridge Regression and the Lasso
-
Ridge: \(\text{min}_{\beta}\left\{ \sum_{i=1}^n(y_i-\beta_0-\sum_{j=1}^p\beta_j x_{ij})^2 \right\}\) subject to $\sum_{j=1}^p\beta_j^2 \le s $
Lasso: \(\text{min}_{\beta}\left\{ \sum_{i=1}^n(y_i-\beta_0-\sum_{j=1}^p\beta_j x_{ij})^2 \right\}\) subject to $\sum_{j=1}^p|\beta_j| \le s $
where the budget s as the regularization parameter ($\lambda\uparrow \equiv s\downarrow$). -
when $p = 2$, then the ridge regression estimates have the smallest RSS out of all points that lie within the circle defined by $\beta_1^2 + \beta_2^2 \le s$, while the lasso estimates have within the diamond defined by $|\beta_1|+|\beta_2| \le s$. when $p = 3$, he constraint region for ridge becomes a sphere, for lasso becomes a polyhedron. For larger p, it becomes a hypersphere and a polytope each. The lasso leads to feature selection due to the sharp corners of its constraint region.
-
the number of predictors that is related to the response is never known a priori for real data sets. A technique such as cross-validation can be used in order to determine which approach is better on a particular data set.
A Simple Special Case
-
An analytical method(solution) for the case when $n = p$, and X a diagonal matrix with 1’s on the diagonal and 0’s in all off-diagonal elements. I.e., the columns of X are orthogonal. Also, assume that we are performing regression without an intercept(or standardized).
(c.f. in real world cases, we need to use numerical methods.) -
The usual least squares, $\hat\beta$ is that minimizes; $\sum_{j=1}^p(y_j-\beta_j)^2$.
and for the ridge, minimizing $\sum_{j=1}^p(y_j-\beta_j)^2+\lambda\sum_{j=1}^p\beta_j^2$.
and for the lasso, minimizing $\sum_{j=1}^p(y_j-\beta_j)^2+\lambda\sum_{j=1}^p|\beta_j|$. -
The ridge regression estiamtes $\hat\beta_j^R = y_j/(1+\lambda)$ and
\(\text{the lasso estimates} \begin{align*} \hat\beta_j^L &= \text{sign}(\hat\beta_j)(|\hat\beta_j|-\lambda)_{+}, \\ \text{or} &= \begin{cases} y_j - \lambda/2, & \mbox{if }y_j > \lambda/2; \\ y_j + \lambda/2, & \mbox{if }y_j < -\lambda/2; \\ 0 & \mbox{if }|y_j| \le \lambda/2. \end{cases} \end{align*}\)
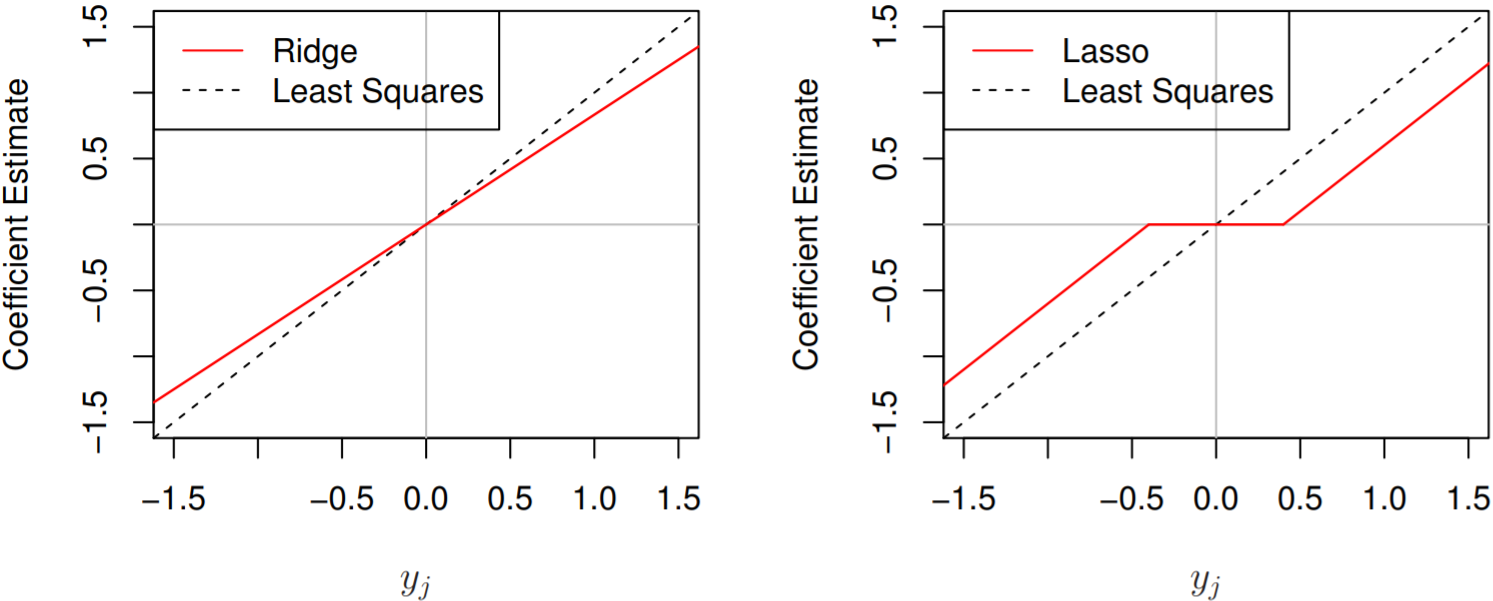
Ridge shrinks all coefficients towards zero by the same “proportion”,
Lasso shrinks all coefficients towards zero by the same “amount”.
Bayesian Interpretation
- $p(\beta|X,Y)\propto f(Y|X,\beta)p(\beta|X) = f(Y|X,\beta)p(\beta)$
with assumption of $p(\beta)=\prod_{j=1}^p g(\beta_j)$ for some density function g.
Two special cases of g:- If g is a Gaussian distribution with mean zero and standard deviation a function of $\lambda$, it follows that the posterior mode for $\beta$, is given by the ridge regression solution. Also, the solution is equal to posterior mean.
- If g is a double-exponential(Laplace) distribution with mean zero and scale parameter a function of $\lambda$, it follows that the posterior mode for $\beta$ is the lasso soultion(which is not the posteriror mean in this case).
- Hence, the lasso expects a priori that many of the coefficients are (exactly) zero, while ridge assumes the coefficients are randomly distributed about zero.
6.3. Dimension Reduction Methods
-
p predictors to M new transformed variables.
Let $Z_m = \sum_{j=1}^p\phi_{jm}X_j$ represent M < p linear combinations of original p predictors. Then fit the linear regression model $y_i = \theta_0 + \sum_{m=1}^M\theta_m z_{im} + \epsilon_i, \quad i = 1, \ldots, n$, using least squares. If the constants $\phi_{1m}, \ldots, \phi_{pm}$ are chosen wisely, dimension reduction approaches can outperform least squares regression. I.e., using least squares, fitting reduced model can lead to better results than fitting the standard linear model. -
\(\sum_{m=1}^M\theta_m z_{im} = \sum_{m=1}^M\theta_m\sum_{j=1}^p\phi_{jm}x_{ij} = \sum_{j=1}^p\sum_{m=1}^M\theta_m\phi_{jm}x_{ij} = \sum_{j=1}^p\beta_j x_{ij},\)
where \(\beta_j = \sum_{m=1}^M\theta_m\phi_{jm}\).
Hence, this model can be a special case of the standard linear regression model. In situations where p is large relative to n, demension reduction methods can significantly reduce the variance of the fitted coefficients. If $M = p$, and all the $Z_m$ are linearly independent, then there are no constraints and the model is equivalent to the standard linear model. -
All dimension reduction methods work in two steps. First, the transformed predictors $Z_m$ are obtained. Second, the model is fit using these M predictors. The choice of $Z_m$, which is, the selection of the $\phi_{jm}$’s can be achieved in different ways.
6.3.1. Principal Components Regression
Principal Components Analysis
-
Goal of PCA:
PCA is a technique for reducing the dimension of an n by p data matrix X, finding small number of dimensions M, which have simillar amount of information to original p predictors. -
The principal component direction of the data is that along which the observations vary the most; with the largest variance of the observations projected onto. The principal component vector $Z_m$ defines the line that is as close as possible to the data, minimizing the sum of the squared perpendicular distances between each point and the line. In other word, the principal component appears to capture most of the information contained in two variables.
-
e.g. in the first principal component,
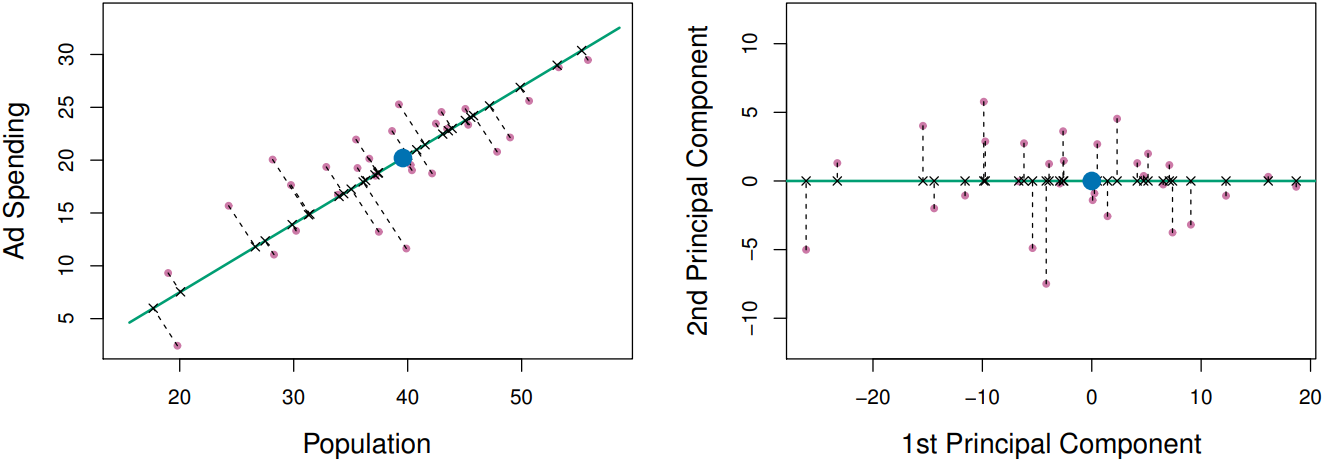
total variance keeped: $Var(X_1)+Var(X_2) = Var(PC_1)+Var(PC_2)$ -
where $X_s$ is $n \times p$ standardized matrix,jth Principal Component Vector of $X_s$: $z_j = X_s v_j$, $\quad j=1,\ldots,p$ is that satisfying \(\text{max}_{\alpha}Var(X_s\alpha)\) subject to \(\lVert\alpha\rVert=1\). Here, the values of $z_{1j}, \ldots, z_{nj}$ are known as the principal component scores.
$v_j$ is $p \times 1$ size eigenvector of $X_s^T X_s$ corresponding to the jth largest eigenvalue, and $\alpha$ is $v_j$’s orthogonality to $v_1,\ldots,v_{j-1}$ ($\alpha^T S v_k = 0$, where S is the sample covariance matrix of $X_s$, or $X_s^T X_s$, and $k = 1, \cdots, j-1$).
Then $z_1 = X_s v_1$, $z_2\bot z_1$, $z_3\bot z_1,z_2$, $\cdots$, $z_p\bot z_1,\ldots,z_{p-1}$. -
derivation
Since $X_s$ is standardized matrix,
\(Var(X_s\alpha) = \alpha^T X_s^T X_s\alpha\)
by Lagrangian form,
\(\begin{align*} \text{max}_{\alpha}Q(X_s,\lambda) &= \text{max}_{alpha}\left[\alpha^T X_s^T X_s\alpha -\lambda\alpha^T\alpha \right] \\ \rightarrow \frac{\partial Q}{\partial\alpha} &= 2X_s^T X\alpha - 2\lambda\alpha \\ \text{for } \hat\alpha, X_s^T X\alpha &= \lambda\alpha \end{align*}\)
note that $\mathbb{A}_v = ev$, the combination of eigenvalue and eigenvector of $\mathbb{A}$.
Thus, $\alpha = v_j$, the jth eigenvector of $X_s^T X_s$, that is, the constraint of orthogonality is satisfied. -
Since PCA has no single solution M;
the proportion of variance explained by mth PC($Z_m$) used:
\(PVE_m = \frac{Var(Z_m)}{\sum_{j=1}^p(Var(Z_j))}\)
(\(\sum_{j=1}^p(Var(Z_j)) = \sum Var(X_j) =\) total variance) -
in SVD of covariance matrix $X^T X$,
\(\begin{align*} X^T X &= \mathbb{VDU}^T\mathbb{UDV}^T \\ &= \mathbb{VD^2 V}^T \end{align*}\)
in this eigen decomposition,
\(\mathbb{V} = (v_1,\ldots,v_p)\) the eigen vectors of $X^T X$
\(\mathbb{D}^2 = \begin{bmatrix} d_1^2 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & d_p^2 \end{bmatrix}\) $d_j^2 = e_j$, jth eigenvalue of $X^T X$
thus,
\(\begin{align*} Var(Z_m) &= \frac{1}{n}(Z_m^T Z_m) \\ &= \frac{1}{n}(v_m^T X_s^T X_s v_m) \\ &= \frac{1}{n}(v_m^T\mathbb{VD}^2\mathbb{V}^T v_m) \\ &= \frac{1}{n}d_m^2 = \frac{1}{n}e_m \end{align*}\) -
Therefore,
\(PVE_m = \frac{Var(Z_m)}{\sum_{j=1}^p(Var(Z_j))} = \frac{e_m}{\sum_{j=1}^p e_j}\)
we can draw a scree plot on the value of $PVE_m$ over the value of m to find optimal “M”.
The Principal Components Regression Approach
-
The key idea is that a small number of principal components can explain most of the variability in the data, as well as the relationship with the response. Under this assumption, fitting a least squares model to $Z_1, \ldots, Z_M$ will lead to better results than fitting a least squares model to $X_1, \ldots, X_p$, since most or all of the information in the data is contained in $Z_m$ and there are smaller number of coefficients, we can mitigate overfitting.
-
Note that PCR is not a feature selection method; is a linear combination of all p of the original features. In this sense, PCR is more closely related to ridge regression than to the lasso.
-
Deciding “M”:
full model is \(\hat{Y} = \hat{\theta}_0 + \hat{\theta}_1 Z_1 + \cdots + \hat{\theta}_p Z_p\)
when $Z_1,\ldots,Z_m$ is from standardized $X_s$ and \(\hat{y}_0 = \bar{y}\),
as $Z_j$’s are orthogonal, adding variable $Z_{j+1}$ does not affect the coefficients. Thus, $\theta_j$’s are not changed by feature selection; that is,
\(\hat{Y} = \hat{\theta}_0 + \hat{\theta}_1 Z_1 \\ \hat{Y} = \hat{\theta}_0 + \hat{\theta}_1 Z_1 + \hat{\theta}_2 Z_2 \\ \vdots \\ \hat{Y} = \hat{\theta}_0 + \hat{\theta}_1 Z_1 +\cdots + \hat{\theta}_p Z_p\) the value of $\theta_k$ is the same.
Then we can use CV methods over these models to get optimal M.
6.3.2. Partial Least Squares
-
The PCR approach identifies linear combinations, or directions, that best represent the predictors. These directions are identified in an unsupervised way, since the response Y is not used to help determine the principal component directions. There, PCR suffers from a drawback: there is no guarantee that the directions that best explain the predictors will also be the best directions to use for predicting the response.
-
PLS is a supervised alternative to PCR; finding PLS directions $Z_1,\ldots,Z_m$ that $Cov(Y,Z_1)\ge Cov(Y,Z_2)\ge\cdots\ge Cov(Y,Z_M)$ instead of $Var(Z_1)\ge\cdots\ge Var(Z_M)$.
-
First PLS direction is computed, after standardizing predictors, by setting each $\phi_{j1}$ equal to the coefficient from the simple linear regression $Y$ onto $X_j$. As $Z_1 = \sum_{j=1}^p\phi_{j1}X_j$, PLS places the highest weight on the variables that are most strongly related to the response.
To find second PLS direction, we adjust each of the variables for $Z_1$, by regressing each variable on $Z_1$ and taking residuals. The residuals can be interpreted as the remaining information that has not been explained by the first PLS direction. Then we compute $Z_2$ using this orthogonalized data by the same way of computing $Z_1$. This predecure repeated M times. -
in Simple Regression case,
$\hat X_j^s$ is a projection of original data $X_j^s$ to a vector $Z_1$; $X_j^s = \alpha Z_1$.
the residual vector $r_j = \hat X_j^s - X_j^s$ and $r_j\bot Z_1$.
Then, $r_j = X_j^{(2)}$ is the orthogonalized data for computing the next $Z_2$. -
The mth PLS direction:
\(\text{max}_{\phi} Cov(y,X_s\phi)\) subject to $\lVert\phi\rVert = 1$, $\phi^T S v_l = 0$
for $\phi$ as orthogonal directions, sample covariance matrix S, and $v_l$ as l th PLS direction.
\(\text{max}_{\phi}[E(\phi^T X_s^T y)-E(y)E(\phi^T X_s)]\), as standardized, $E(X_s) = 0$,
\(\equiv \text{max}_{\phi}\phi^T \dot X_s^T y\) is maximization of dot product of 2 vectors.
note that, when two vectors are in the same direction, dot product is maximized.
$\therefore \phi=X_s^T y$.
6.4. Considerations in High Dimensions
6.4.1. High-Dimensional Data
- Data sets that containing more features than observations, $p > n$.
6.4.2. What Goes Wrong in High Dimensions?
- Standard least squares cannot be performed. Regardless of the true relationship between features and response, least squares will result in a perfect fit to the data, lead to overfitting of the data and poor predictions.
6.4.3. Regression in High Dimensions
- new technologies that allow for the collection of measurements for thousands or millions of features are a double-edged sword: they can lead to improved predictive models if these features are in fact relevant to the problem at hand, but will lead to worse results if the features are not relevant. Even if they are relevant, the variance incurred in fitting their coefficients may outweigh the reduction in bias that they bring.
6.4.4. Interpreting Results in High Dimensions
-
In high-dimensional setting, the multicollinearity problem is extreme:
any variable in the model is a linear combination of all of the other variables in the model. This means we can never know exactly which variables truly are predictive of the outcome, and we can never identify the best coefficients for use in the regression. -
When $p > n$, it is easy to obtain a a useless model that has zero residuals. Therefore, we should never use sum of squared errors, p-values, $R^2$ statistics, or other traditional measures of model fit on the training data as evidence of a good model fit. Instead we report results on an independent test set, or cross-validation errors.