Attention

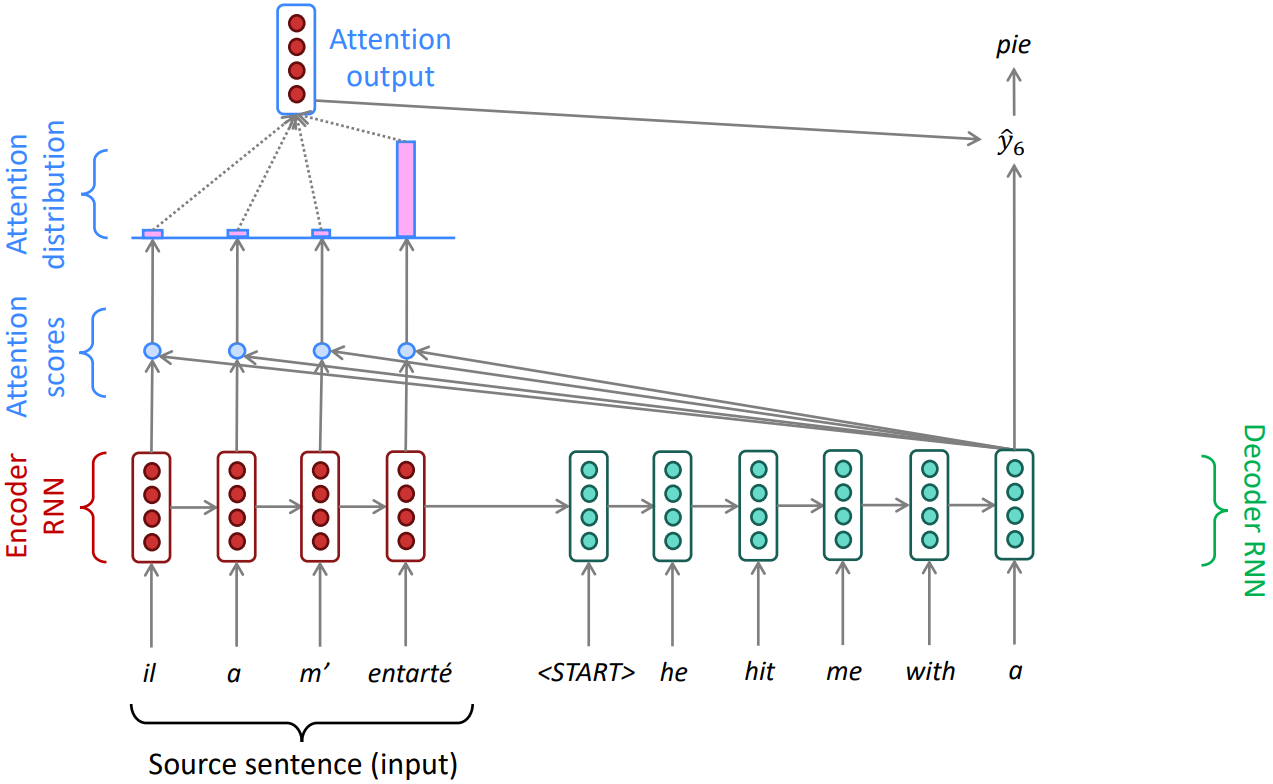
• Encoder hidden states $\mathbf{h}_1, \ldots, \mathbf{h}_N \in \mathbb{R}^h$
• On timestep $t$, we have Decoder hidden state $\mathbf{s}_t \in \mathbb{R}^h$
• Attention score $\mathbf{e}^t$ for this step:
  \(\mathbf{e}^t = \left[ \mathbf{s}_t^T \mathbf{h}_1, \ldots, \mathbf{s}_t^T \mathbf{h}_N \right] \in \mathbb{R}^N\)
• Take softmax to get the Attention distribution:
  \(\alpha^t = \text{softmax}(\mathbf{e}^t) \in \mathbb{R}^N\)
• Use $\alpha^t$ to take a weighted sum of the encoder hidden states to get the Attention output:
  \(\mathbf{a}_t = \sum_{i=1}^N \alpha_i^t \mathbf{h}_i \in \mathbb{R}^h\)
• Finally, concatenate the attention output $\mathbf{a}_t$ with the decoder hidden state $s_t$ and proceed as in the non-attention seq2seq model
  \(\left[ \mathbf{a}_t ; \mathbf{s}_t \right] \in \mathbb{R}^{2h}\)

Attention is great

• Attention significantly improves NMT performance
  Allow decoder to focus on certain parts of the source
• Attention provides more “human-like” model of the MT process
  You can look back at the source sentence while translating, rather than needing to remember it all
• Attention solves the bottleneck problem
  Attention allows decoder to look directly at source; bypass bottleneck
• Attention helps with the vanishing gradient problem
  Provides shortcut to faraway states
• Attention provides some interpretability
  By inspecting attention distribution, we can see what the decoder was focusing on; we can get (soft) alignment for free. Without explicitly trained an alignment system, the network just learned alignment by itself

Attention variants

• With some values \(\mathbf{h}_1, \ldots, \mathbf{h}_N \in \mathbb{R}^{d_1}\) and a query \(\mathbf{s} \in \mathbb{R}^{d_2}\),
  Attention always involves:
  1. Computing the attention scores $\mathbf{e}\in\mathbb{R}^N$
  2. Taking softmax to get attention distribution:
  $\alpha = \text{softmax}(\mathbf{e})\in\mathbb{R}^N$
  3. Take weighted sum of values to get attention output:
  $\mathbf{a} = \sum_{i=1}^N \alpha_i \mathbf{h}_i \in \mathbb{R}^{d_1}$

$\rightarrow$ There are multiple ways to compute attention scores $\mathbf{e}\in \mathbb{R}^N$ from $\mathbf{h}_1, \ldots, \mathbf{h}_N \in \mathbb{R}^{d_1}$ and $\mathbf{s} \in \mathbb{R}^{d_2}$:

• Basic dot-product attention: $\mathbf{e}_i = \mathbf{s}^T \mathbf{h}_i \in \mathbb{R}$
  • What we saw earlier, assume that $d_1 = d_2$.
• Multiplicative attention: $\mathbf{e}_i = \mathbf{s}^T \mathbf{W} \mathbf{h}_i \in \mathbb{R}$
  • Luong, Pham, and Manning 2015
  • Where $\mathbf{W} \in \mathbb{R}^{d_2 \times d_1}$ is a weight matrix of learnable parameters(but too many!)
• Reduced rank multiplicative attention: $e_i = \mathbf{s}^T(\mathbf{U}^T \mathbf{V})h_i = (\mathbf{U}s)^T (\mathbf{V}h_i)$
  • low rank matrices $\mathbf{U} \in \mathbb{R}^{k\times d_2}$, $\mathbf{V} \in \mathbb{R}^{k\times d_1}$, $k \ll d_1, d_2$
• Additive attention: $\mathbf{e}_i = \mathbf{v}^T \tanh (\mathbf{W}_1 \mathbf{h}_i + \mathbf{W}_2 \mathbf{s}) \in \mathbb{R}$
  • Bahdanau, Cho, and Bengio 2014
  • Where $\mathbf{W}_1 \in \mathbb{R}^{d_3 \times d_1}$, $\mathbf{W}_2 \in \mathbb{R}^{d_3 \times d_2}$ are weighted matrices and $\mathbf{v} \in \mathbb{R}^{d_3}$ is a weight vector.
  • $d_3$ (the attention dimensionality) is a hyperparameter
  • “Additive” is a weird name; it’s really using a neural net layer.

Attention is a general Deep Learning technique

Attention is a great way to improve the sequence-to-sequence model for Machine Translation. However, you can use attention in many architectures (not just seq2seq) and many tasks (not just MT)

More general definition of attention:

• Given a set of vector values, and a vector query, attention is a technique to compute a weighted sum of the values, dependent on the query.

• We sometimes say that the query attends to the values. A kind of memory access mechanism.

• Intuition:
  • The weighted sum is a selective summary of the information contained in the values, where the query determines which values to focus on.
  • Attention is a way to obtain a fixed-size representation of an arbitrary set of representations (the values), dependent on some other representation (the query).
• Upshot:
  • Attention has become the powerful, flexible, general way pointer and memory manipulation in deep learning models. A new idea from after 2010!