cs224n - Lecture 9. Self-Attention and Transformers
So far: recurrent models for (most) NLP
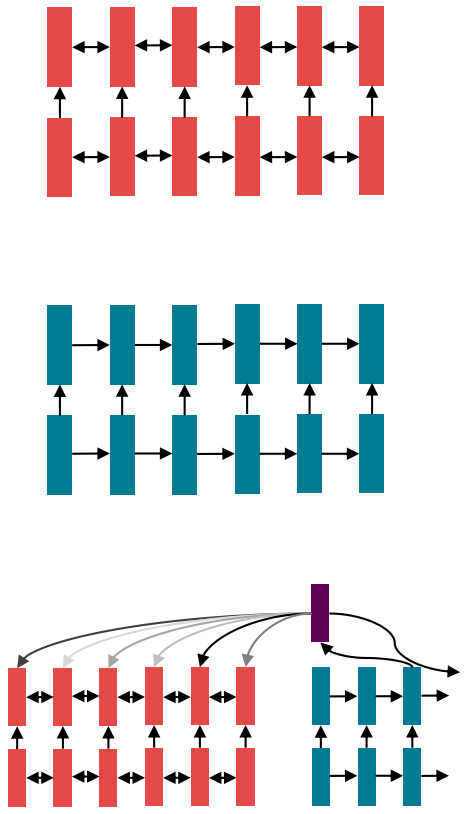
- Circa 2016, the de facto strategy in NLP is to encode
sentences with a bidirectional LSTM.
(for example, the source sentence in a translation)
- Define your output (parse, sentence, summary) as a sequence, and use an (unidirectional) LSTM to generate it.
- Use attention to allow flexible access to memory.
-
Seq2Seq models need to process variable-length inputs into fixed-length representations
-
To deal with seq2seq problems, we learned end-to-end differentiable system using an encoder-decoder architecture.
-
Instead of entirely new ways of looking at problems, we’re trying to find the best building blocks to plug into our models and enable broad progress.
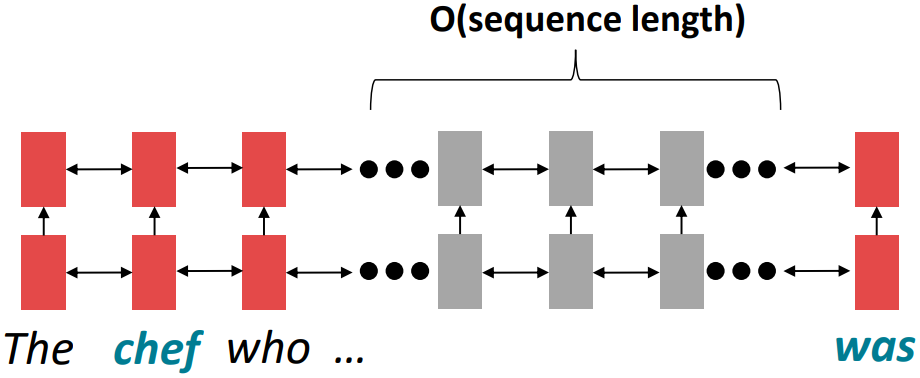
Issues with recurrent models: Linear interaction distance
- RNNs are unrolled “left-to-right”:
This encodes linear locality: a useful heuristic- Nearby words often affect each other’s meanings
- Problem: RNNs take O(sequence length) steps for distant word pairs to interact.
- Hard to learn long-distance dependencies (because gradient problems)
- Linear order of words is “baked in”; linear order isn’t the right way to think about sentences
Issues with recurrent models: Lack of parallelizability
- Forward and backward passes have O(sequence length) unparallelizable operations
- Future RNN hidden states can’t be computed in full before past RNN hidden states have been computed; not GPU friendly, inhibits training on very large datasets.
Alternatives: Word windows
- Word window models aggregate local contexts (Also known as 1D convolution)
- Number of unparallelizable operations does not increase sequence length
(O(1) dependence in time)
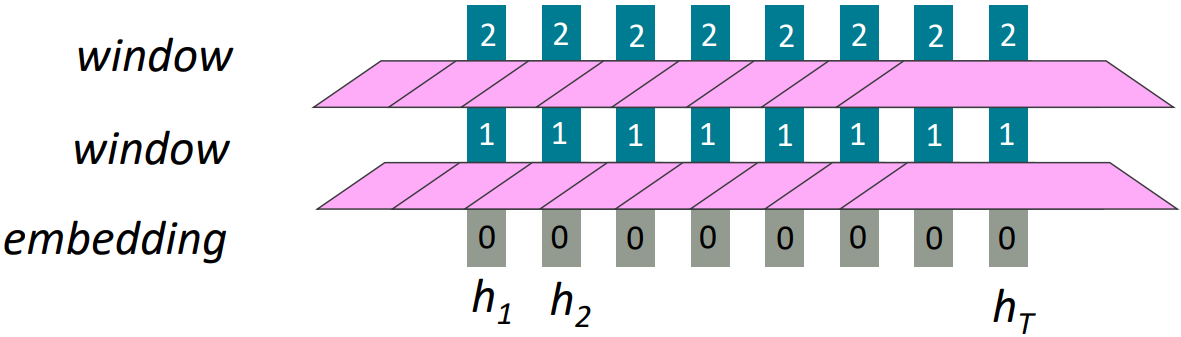
- Number of unparallelizable operations does not increase sequence length
- What about in long-distance dependencies?
- Stacking word window layers allows interaction between farther words
- Maximum Interaction distance = sequence length / window size
But if your sequences are too long, you’ll just ignore long-distance context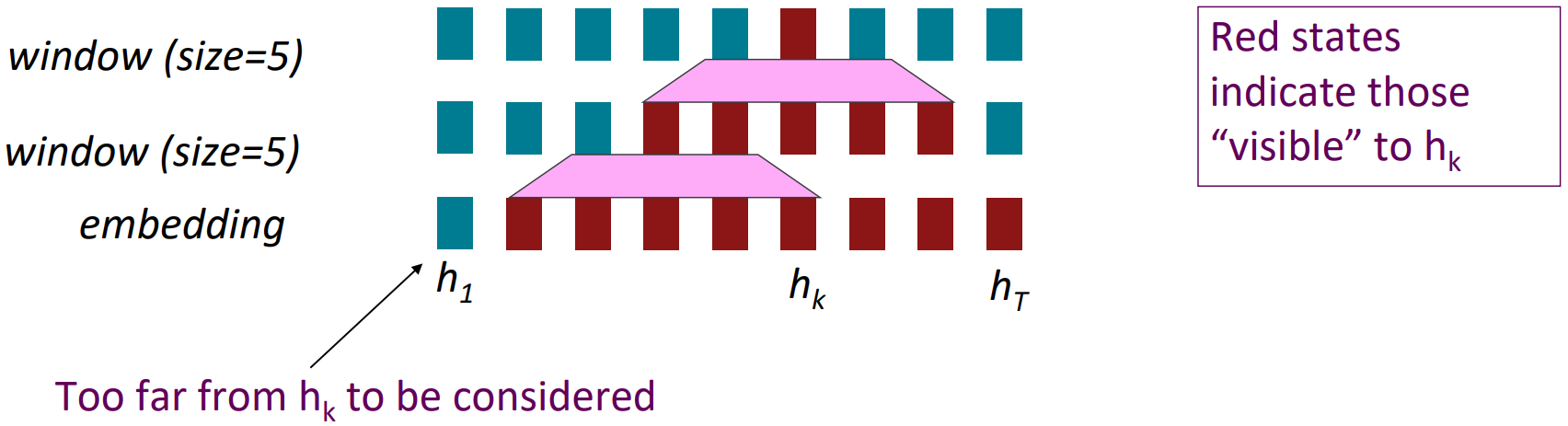
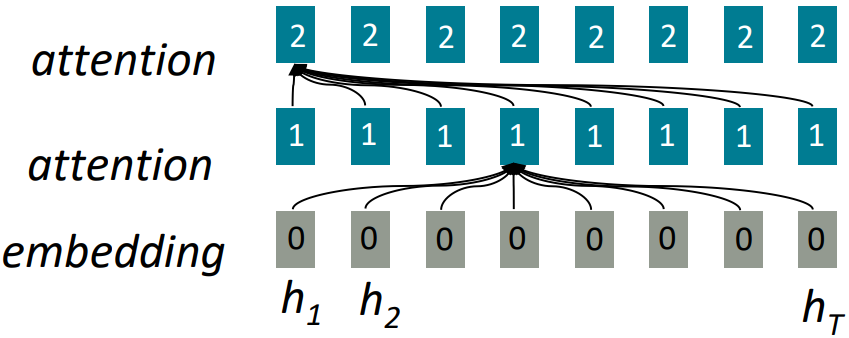
Alternatives: Attention
- Attention treats each word’s representation as a query to access and
incorporate information from a set of values.
- Out of the encoder-decoder structure; think about attention within a single sentence.
- Number of unparallelizable operations does not increase sequence length; not parallelizable in depth but parallelizable in time.
- Maximum interaction distance: O(1), since all words interact at every layer
Self-Attention
- Recall: Attention operates on queries, keys, and values.
- queries: $q_1, q_2, \ldots, q_T \in \mathbb{R}^d$
- keys: $k_1, k_2, \ldots, k_T \in \mathbb{R}d$
- values: $v_1, v_2, \ldots, v_T \in \mathbb{R}d$
-
In self-attention, the queries, keys, and values are drawn from the same source.
For example, if the output of the previous layer is $x_1, \ldots, x_T$ (one vec per word), we could let $v_i = k_i = q_i = x_i$ (use the same vectors for all of them). - The (dot product) self-attention operation is as follows:
- Compute key-query affinities: $e_{ij} = q_i^T k_j $
- Compute attention weights from affinities(softmax):
\(\begin{align*} \alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{j^\prime} \exp(e_{ij^\prime})} \end{align*}\) - Compute outputs as weighted sum of values
\(\begin{align*} \text{output}_i = \sum_j \alpha_{ij}v_j \end{align*}\)
- Q: FCN vs Self-Attention?
Self-attention as an NLP building block
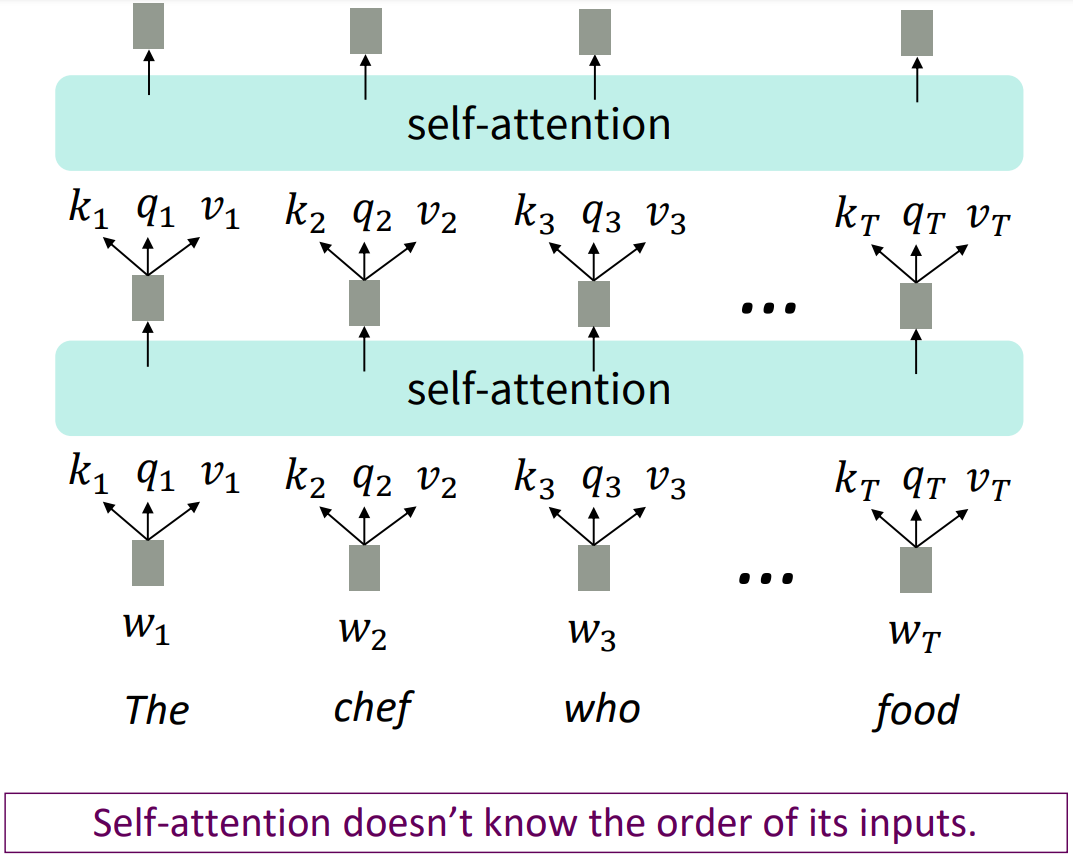
- Can self-attention replace the recurrence? NO.
Sequence order
- Self-attention is an operation on sets; it has no inherent notion of order.
- To fix this, encode the order of the sentence.
-
Consider representing each sequence index as a vector;
$p_i \in \mathbb{R}^d$, for \(i \in \left\{ 1,2,\ldots, T \right\}\) are position vectors - Let $\tilde{v}_i, \tilde{k}_i, \tilde{q}_i$ be our old inputs, then add $p_i$ to inputs;
$v_i = \tilde{v}_i + p_i$
$q_i = \tilde{q}_i + p_i$
$k_i = \tilde{k}_i + p_i$- In deep self-attention networks, we do this at the first layer; you could concatenate them as well, but mostly, just add.
- Position representation vectors through sinusoids
- Sinusoidal position representations: concatenate sinusoidal functions of varying periods
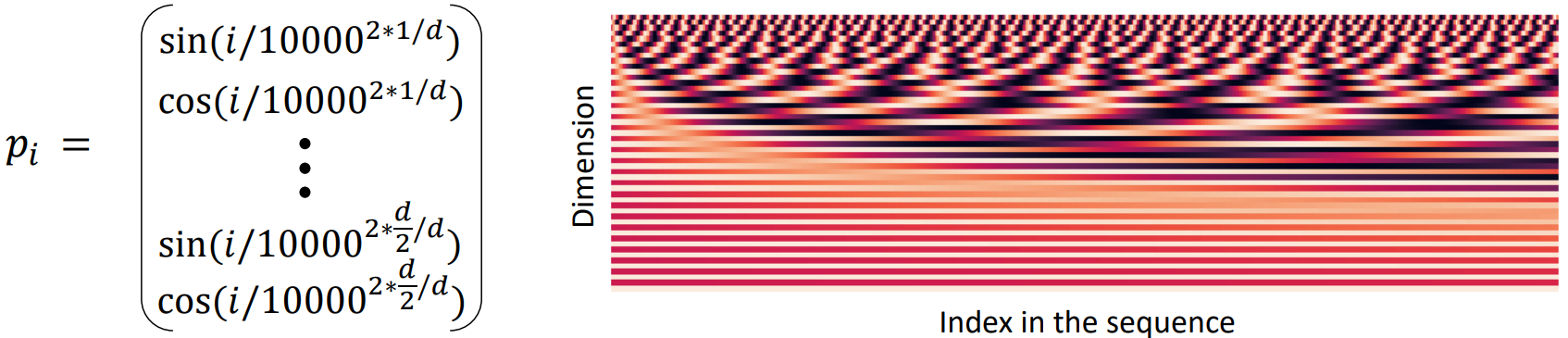
- Pros:
- Periodicity indicates that maybe “absolute position” isn’t as important
- Maybe can extrapolate to longer sequences as periods restart!
- Cons:
- Not learnable; also the extrapolation doesn’t really work!
- Sinusoidal position representations: concatenate sinusoidal functions of varying periods
- Position representation vectors learned from scratch
- Learned absolute position representations: Let a matrix $p \in \mathbb{R}^{d \times T}$ and each learnable parameters $p_i$ be a column of that matrix; Most systems use this!
- Pros:
- Flexibility: each position gets to be learned to fit the data
- Cons:
- Definitely can’t extrapolate to indices outside $1, \ldots, T$.
- Some more flexible representations of position:
- Relative linear position attention (Shaw et al., 2018)
- Dependency syntax-based position (Wang et al., 2019)
Nonlinearities
-
There are no elementwise nonlinearities in self-attention; stacking more self-attention layers just re-averages value vectors.
-
Easy fix: add a feed-forward network to post-process each output vector.
(Self-Att. - FF - Self-Att. - FF - ...)
\(\begin{align*} m_i &= MLP(\text{output}_i) \\ &= W_2 \ast \text{ReLU}(W_1 \times \text{output}_i + b_1) + b_2 \end{align*}\)
Masking the future
-
To use self-attention in decoders, we need to ensure we don’t “look at the future” when predicting a sequence.
-
Easily: at every timestep, we could change the set of keys and queries to include only past words. But it’s inefficient dealing with tensors, not parallelizable.
-
Instead, to enable parallelization, mask out attention to future words by setting attention scores to $-\infty$ (attention weights to 0).
$e_{ij} = \begin{cases} q_i^T k_j, & j < i
-\infty, & j \ge i \end{cases}$

Recap: Necessities for a self-attention building block
- Self-attention: the basis of the method
- Position representations:
Specify the sequence order, since self-attention is an unordered function of its inputs. - Nonlinearities:
At the output of the self-attention block, frequently implemented as a simple feed-forward network. - Masking:
In order to parallelize operations while not looking at the future, keeps information about the future from “leaking” to the past.
Transformer
- The Transformer Encoder-Decodr (Vaswani et al., 2017)
At a high level look;
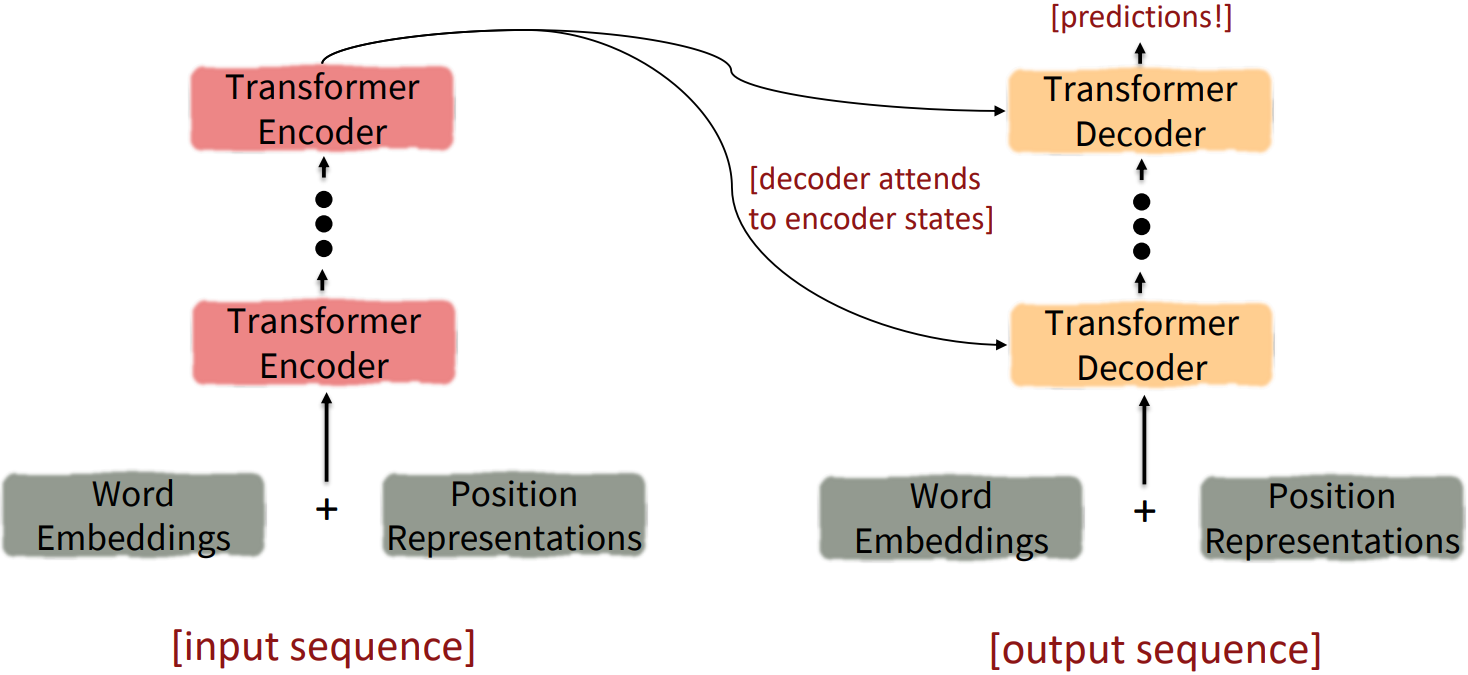
- What’s left in a Transformer Encoder Block:
- Key-query-value attention: How do we get input vectors from a single word embedding?
- __Multi-headed attention: Attend to multiple places in a single layer
- Tricks to help with training:
- Residual connections
- Layer normalization
- Scaling the dot product These tricks don’t improve what the model is able to do; they help improve the training process. Both of these types of modeling improvements are very important.
The Transformer Encoder: Key-Query-Value Attention
- Let $x_1, \ldots, x_T \in \mathbb{R}^d$ be input vectors to the Transformer encoder. Then keys, queries, values are:
- $k_i = Kx_i$, where $K \in \mathbb{R}^{d \times d}$ is the key matrix.
- $q_i = Qx_i$, where $Q \in \mathbb{R}^{d \times d}$ is the query matrix.
- $v_i = Vx_i$, where $V \in \mathbb{R}^{d \times d}$ is the value matrix.
These matrices (of learnable parameters) allow different aspects of the $x$ vectors to be used/emphasized in each of the three roles.
- Computed in matrices,
- Let $X = \left[ x_1; \ldots; x_T \right] \in \mathbb{R}^{T\times d}$ be the concatenation of input vectors.
- First, note that $XK \in \mathbb{R}^{T\times d}$, $XQ \in \mathbb{R}^{T\times d}$, $XV \in \mathbb{R}^{T\times d}$.
- The output tensor is defined as $\text{output} = \text{softmax}(XQ(XK)^T) \times XV$.
- Take the query-key dot products in one matrix multiplication: $XQ(XK)^T = XQK^T X^T \in \mathbb{T}^{T\times T} $ (All pairs of attention scores)
- Take softmax, and compute the weighted average with another matrix multiplication: $\text{output} \in \mathbb{T}^{T\times d}$
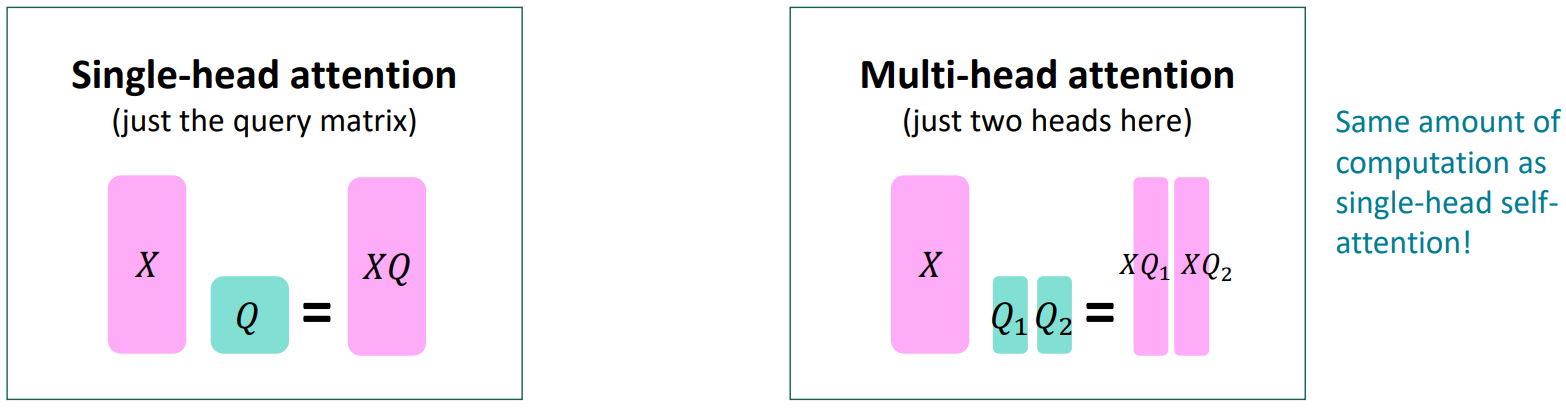
The Transformer Encoder: Multi-headed attention
- What if we want to look in multiple places in the sentence at once?
- For word $i$, self-attention “looks” where $x_i^T Q^T K x_j$ is high, but maybe we want to focus on different $j$ for different reasons?
- Define multiple attention “heads” through multiple $Q, K, V$ matrices:
- Let $Q_l, K_l, V_l \in \mathbb{R}^{d\times \frac{d}{h}}$, where $h$ is the number of attention heads, and $l$ ranges from $1$ to $h$.
- Each attention head performs attention independently:
$\text{output}_l = \text{softmax}(XQ_l K_l^T X^T) \ast X V_l \in \mathbb{R}^{d/h}$ - Then combine the all outputs from the heads:
$\text{output} = Y\left[ \text{output}_1; \ldots, \text{output}_h \right]$, where $Y \in \mathbb{R}^{d\times d}$. - Each head gets to “look” at different things and construct value vectors differently.
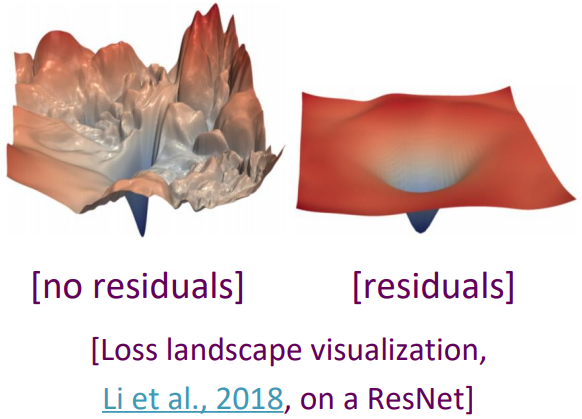
The Transformer Encoder: Residual connections [He et al., 2016]
-
Residual connections are a trick to help models train better.
-
Instead of $X^{(i)} = \text{Layer}(X^{(i-1)})$ (where $i$ represents the layer)
We let $X^{(i)} = X^{(i-1)} + \text{Layer}(X^{(i-1)})$ (so we only have to learn “the residual” from the previous layer) - Solves vanishing gradient problem
- Residual connections are thought to make the loss landscape considerably smoother (thus easier training!)
The Transformer Encoder: Layer normalization [Ba et al., 2016]
- Layer normalization is a trick to help models train faster.
- Idea: cut down on uninformative variation in hidden vector values by normalizing to unit mean and standard deviation within each layer.
- LayerNorm’s success may be due to its normalizing gradients (Xu et al., 2019)
- Let $x\in \mathbb{R}^d$ be an individual (word) vector in the model.
- Let the mean $\mu = \sum_{j=1}^d x_j \in \mathbb{R}$
- Let the standard deviation $\sigma = \sqrt{\frac{1}{d}\sum_{j=1}^d (x_j-\mu)^2} \in \mathbb{R}$
- Let $\gamma \in \mathbb{R}^d$ and $\beta \in \mathbb{R}$ be learned “gain” and “bias” parameters (Can omit)
- Then layer normalization computes:
\(\begin{align*}\text{output} = \frac{x-\mu}{\sigma + \epsilon}\ast\gamma + \beta \end{align*}\);
(Normalize by scalar mean and variance, and modulate by learned elementwise gain and bias)
The Transformer Encoder: Scaled Dot Product [Vaswani et al., 2017]
-
When dimensionality $d$ becomes large, dot products between vectors tend to become large.
Because of this, inputs to the softmax function can be large, making the gradients small (leading to saturate region) -
Instead of the self-attention functiopn we’ve seen:
$\text{output}_l = \text{softmax}(XQ_l K_l^T X^T) \ast X V_l$
We divide the attention scores by $\sqrt{d/h}$, to stop the scores from becoming large just as a function of $d/h$ (The dimensionality divided by the number of heads.):
$\text{output}_l = \text{softmax}(\frac{XQ_l K_l^T X^T}{\sqrt{d/h}}) \ast X V_l$
Now look at the Decoder Blocks
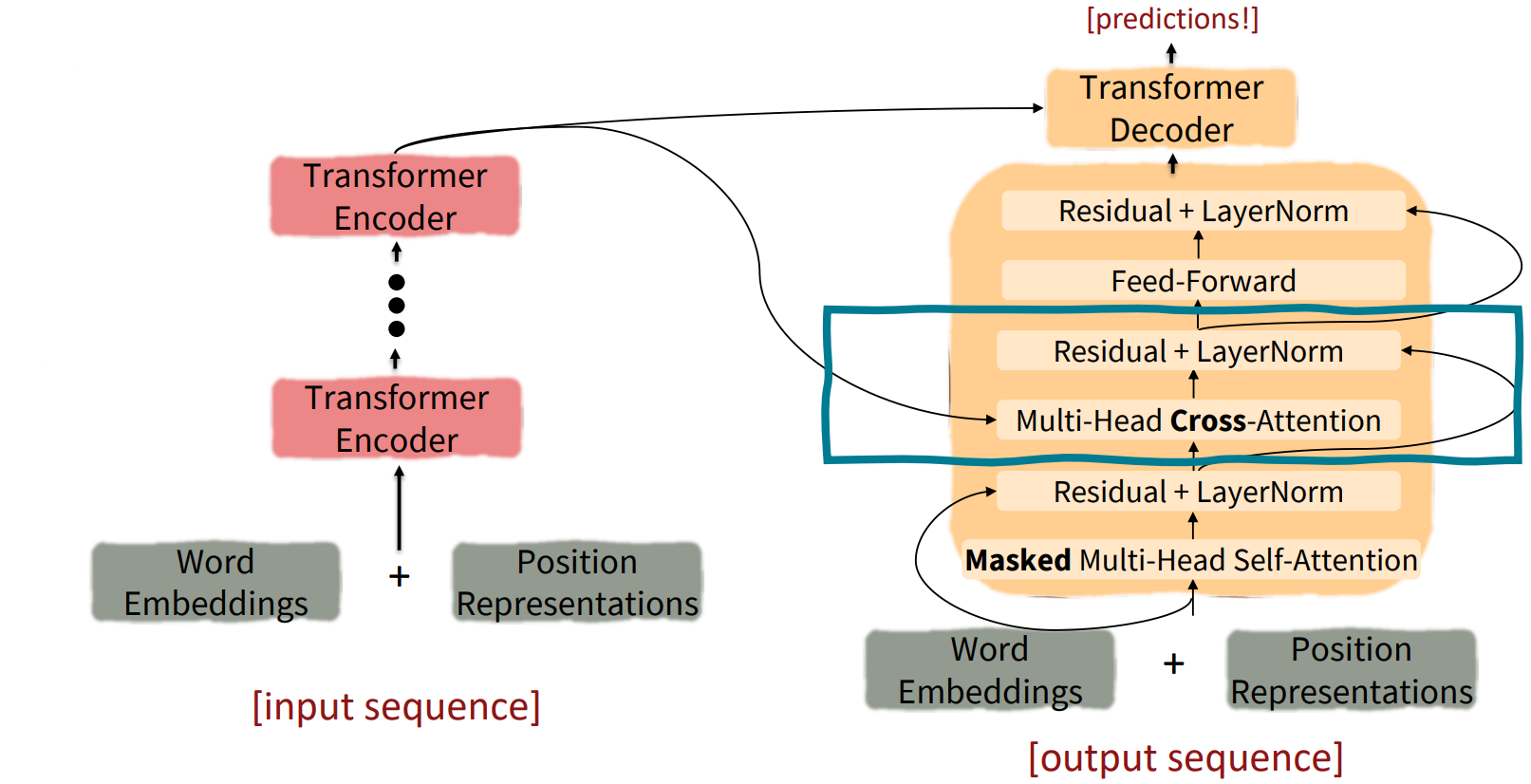
The Transformer Decoder: Cross-attention (details)
-
Let $h_1, \ldots, h_T$ be output vecotrs from the Transformer encoder (the last block); $x_i \in \mathbb{R}^d$
Let $z_1, \ldots, z_T$ be input vectors from the Transformer decoder, $z_i\in \mathbb{R}^d$
Then keys and values are drawn from the encoder (like a memory); $k_i = Kh_i, v_i = Vh_i$
The queries are drawn from the decoder; $q_i = Qz_i$ -
In matrices:
- Let $H = \left[ h_1; \ldots, h_T \right] \in \mathbb{R}^{T\times d}$ be the concatenation of encoder vecotrs.
- Let $Z = \left[ z_1; \ldots, z_T \right] \in \mathbb{R}^{T\times d}$ be the concatenation of decoder vectors.
- The output is defined as $\text{output} = \text{softmax}(ZQ(HK)^T)\times HV$.
What would we like to fix about the Transformer?
- Quadratic compute in self-attention:
- Computing all pairs of interactions means our computation grows quadratically with the sequence length.
- For recurrent models, it only grew linearly.
- Position representations:
- Are simple absolute indices the best we can do to represent position?
- Relative linear position attention (Shaw et al., 2018)
- Dependency syntax-based position (Wang et al., 2019)
Quadratic computation as a function of sequence length
- One of the benefits of self-attention over recurrence was that it’s highly parallelizable.
However, its total number of operations grows as $O(T^2 d)$, where $T$ is the sequence length, and $d$ is the dimensionality.
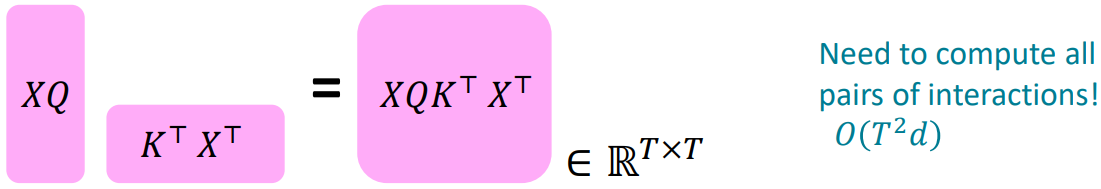
- Think of $d$ as around 1,000.
So, for a single (shortish) sentence, $T \le 30; T^2 \le$ 900.
In practice, we set a bound like $T = 512$.
But what if we’d like $T\ge 10,000$? to work on long documents?
Recent work on improving on quadratic self-attention cost
-
Considerable recent work has gone into the question,
Can we build models like Transformers without paying the $O(T^2)$ all-pairs self-attention cost? - Linformer (Wang et al., 2020)
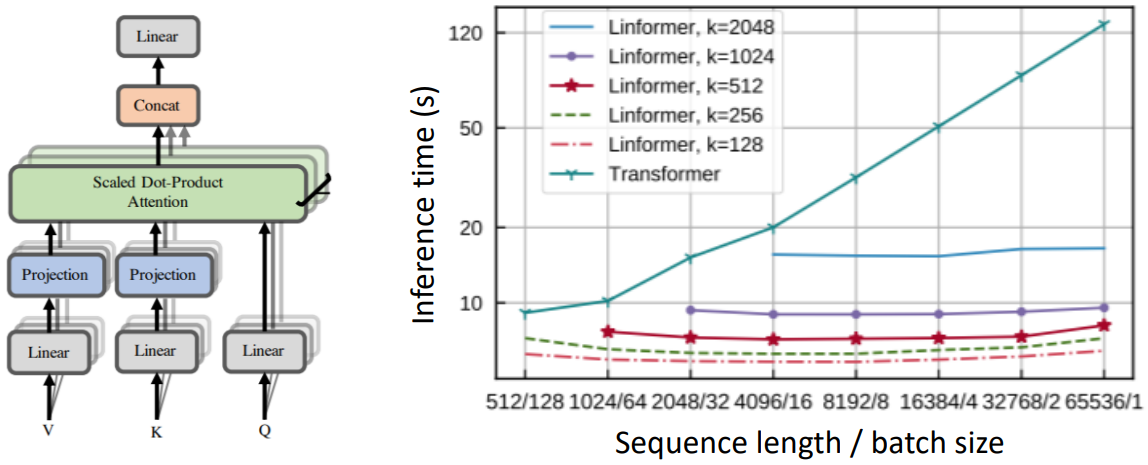
- Key idea: map the sequence length dimension to a lower-dimensional space for values, keys.
- BigBird (Zaheer et al., 2021)
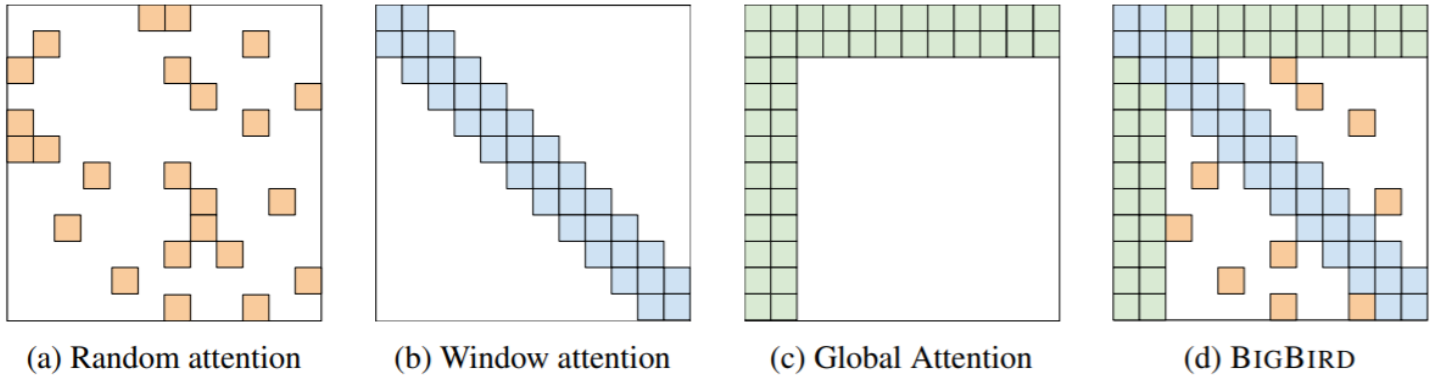
- Key idea: replace all-pairs interactions with a family of other interactions, like local windows, looking at everything, and random interactions.