Objectives

1. The foundations of the effective modern methods for deep learning applied to NLP; from basics to key methods used in NLP: RNN, Attention, Transformers, etc.)
2. A big picture understanding of human languages and the difficulties in understanding and producing them
3. An understanding of and ability to build systems (in PyTorch) for some of the major problems in NLP: Word meaning, dependency parsing, machine translation, question answering
   

• NLP tasks:
  Easy: Spell Checking, Keyword Search, Finding Synonyms
  Medium: Parsing information from websites, documents, etc.
  Hard: Machine Translation, Semantic Analysis, Coreference, QA

Word meaning

• Commonest linguistic way of thinking of meaning:
  signifier (symbol) $\Leftrightarrow$ signified (idea or thing)
  $=$ denotational semantics

• Common NLP solution: Use, e.g., WordNet, a thesaurus containing lists of synonym sets and hypernyms(“is a” relationships).

• Problems with resources like WordNet

  • Great as a resource but missing nuance
  • Missing new meanings of words; impossible to keep up-to-date
  • Subjective
  • Requires human labor to create and adapt
  • Can’t compute accurate word similarity

Representing words as discrete symbols

• In traditional NLP, we regard words as discrete symbols - a localist representation.
  $\rightarrow$ in a statistical machine learning systems, such symbols for words are separately represented by one-hot vectors. Thus we need to have huge vector dimension corresponding to the number of words in vocabulary.
  • But with discrete symbols, two vectors are orthogonal and there is no natural notion of similarity for one-hot vectors.
• Solution:
  • Could try to rely on WordNet’s list of synonyms to get similarity?
    But it is well-known to fail badly; incompleteness, etc.
  • Instead: learn to encode similarity in the vecotr themselves.

Representing words by their context

• Distributional semantics: A word’s meaning is given by the words that frequently appear close-by
  • “You shall know a word by the company it keeps” (J. R. Firth 1957:11)
  • One of the most successful ideas of modern statistical NLP
• When a word w appears in a text, its context is the set of words that appear nearby(within a fixed-size window).
• Use the many contexts of w to build up a representation of w

Word vectors

• A dense vector for each word, chosen so that it is similar to vectors of words that appear in similar contexts

• Note: as a distributed representation, word vectors are also called word embeddings or (neural) words representations

Word2vec

Word2vec: overview

• Word2vec(Mikolov et al. 2013) is a framework for learning word vectors
• idea:
  • We have a large corpus(“body”) of text
  • Every word in a fixed vocabulary is representated by a vector
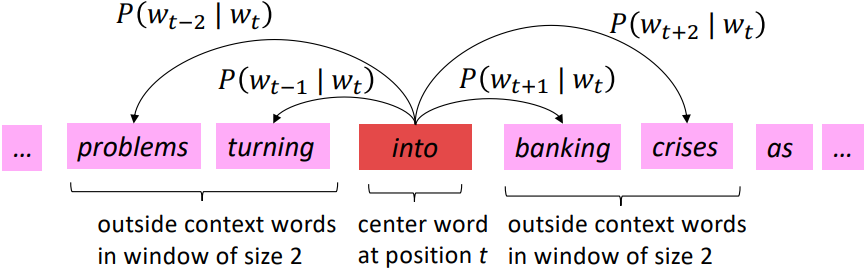
  • Go through each position t in the text, which has a center word c and context(“outside”) words o
  • Use the similarity of the word vectors for c and o to calculate the probability of o given c(or vice versa)
  • Keep adjusting the word vectors to maximize this probability

We can learn these word vectors from just a big pile of text by doing this distributional similarity task of being able to predict what words occur in the context of other words.

• Example windows and process for computing $P(w_{t+j}|w_t)$
  

Word2vec: objective function

For each position $t = 1, \ldots, T$, predict context words within a window of fixed size m, given center word $w_j$. Data likelihood:
\(\begin{align*} L(\theta) = \prod_{t=1}^T \prod_{\substack{-m\leqq j\leqq m \\ j\ne 0}} P(w_{t+j}|w_t;\theta) \end{align*}\)
where $\theta$ is all variables to be optimized.

The objective function $J(\theta)$ is the (average) negative log likelihood:
\(\begin{align*} J(\theta) = -\frac{1}{T}\log L(\theta) = -\frac{1}{T}\sum_{t=1}^T \sum_{\substack{-m\leqq j\leqq m \\ j\ne 0}}\log P(w_{t+j}|w_t;\theta) \end{align*}\)
Minimizing objective function $\Leftrightarrow$ Maximizing predictive accuracy

• Question: How to calculate $P(w_{t+j}\vert w_t;\theta)$?
• Answer: We will use two vectors per word w:
  • $v_w$ when w is a center word
  • $u_w$ when w is a context word
• Then for a centor word c and a context word o:
  \(P(o|c) = \frac{\exp(u_o^T v_c)}{\sum_{w \in V}\exp(u_w^T v_c)}\)

Word2vec: prediction function

\(P(o|c) = \frac{\exp(u_o^T v_c)}{\sum_{w \in V}\exp(u_w^T v_c)}\)

1. $u_w^T v_c$: Dot product compares similarity of o and c.
   $u^T v = u\ .v = \sum_{i=1}^n u_i v_i$
   Larger dot product = larger probability
2. $\exp$: Exponentiation makes anything positive
3. $\sum_{w \in V}\exp(u_w^T v_c)$: Normalize over entire vocabulary to give probability distribution.

• This is an example of the softmax function $\mathbb{R}^n \rightarrow (0,1)^n$(Open region) that maps arbitary values $x_i$ to a probability distribution $p_i$
  \(\mbox{softmax}(x_i) = \frac{\exp(x_i)}{\sum_{j=1}^n\exp(x_j)} = p_i\)

• To train the model: Optimize value of parameters to minimize loss

  • Recall: $\theta$ represents all the model parameters, in one long vector
  • In our case, with d-dimensional vectors and V-many words, we have: $\theta \in \mathbb{R}^{2dV}$
  • Remember: every word has two vectors
  • We optimize these parameters by walking down the gradient(gradient descent)
  • We compute all vector gradients

Word2vec derivations of gradient

\(\begin{align*} J(\theta) = -\frac{1}{T}\log L(\theta) = -\frac{1}{T}\sum_{t=1}^T \sum_{\substack{-m\leqq j\leqq m \\ j\ne 0}}\log P(w_{t+j}|w_t;\theta) \end{align*}\)
\(P(o|c) = \frac{\exp(u_o^T v_c)}{\sum_{w \in V}\exp(u_w^T v_c)}\)

\(\frac{\partial}{\partial v_c} \log \frac{\exp(u_o^T v_c)}{\sum_{w \in V}\exp(u_w^T v_c)} = \underbrace{\frac{\partial}{\partial v_c} \log \exp(u_o^T v_c)}_{(1)} - \underbrace{\frac{\partial}{\partial v_c} \log \sum_{w=1}^V \exp(u_w^T v_c)}_{(2)}\)
\(\begin{align*}\cdots (1) &= \frac{\partial}{\partial v_c} u_o^T v_c \\ &= u_o \end{align*}\)
\(\begin{align*}\cdots (2) &= \frac{1}{\sum_{w=1}^V \exp(u_w^T v_c)} \cdot \sum_{x=1}^V \frac{\partial}{\partial v_c} \exp(u_x^T v_c) \\ &= \frac{1}{\sum_{w=1}^V \exp(u_w^T v_c)} \cdot \sum_{x=1}^V \exp(u_x^T v_c) \cdot \frac{\partial}{\partial v_c} u_x^T v_c \\ &= \frac{1}{\sum_{w=1}^V \exp(u_w^T v_c)} \cdot \sum_{x=1}^V \exp(u_x^T v_c) \cdot u_x \\ \end{align*} \\\)
\(\begin{align*} \frac{\partial}{\partial v_c} \log P(o|c) &= u_o - \frac{\sum_{x=1}^V \exp(u_x^T v_c)u_x}{\sum_{w=1}^V \exp(u_w^T v_c)} \\ & = u_o - \sum_{x=1}^V \underbrace{\frac{\exp(u_x^T v_c)}{\sum_{w=1}^V \exp(u_w^T v_c)}}_{\mbox{softmax formula}} u_x \\ & = u_o - \underbrace{\sum_{x=1}^V P(x|c) u_x}_{\mbox{Expectation}} \\ & = \mbox{observed} - \mbox{expected} \end{align*}\)