cs231n - Lecture 12. Generative Models
Supervised vs. Unsupervised
-
Supervised Learning:
Data: $(x,y)$; y is label
Goal: Learn a function to map $x\rightarrow y$ -
Unsupervised Learning:
Data: x; no labels
Goal: Learn some underlying hidden structure of the data
Generative Modeling
Given training data, generate new samples from same distribution
- Objectives:
- Learn $p_{\scriptstyle\text{model}}(x)$ that approximates $p_{\scriptstyle\text{data}}(x)$
- Sampling new x from $p_{\scriptstyle\text{model}}(x)$
- Formulate as density estimation problems:
- Explicit density estimation: explicitly define and solve for $p_{\scriptstyle\text{model}}(x)$.
- Implicit density estimation: learn model that can sample from $p_{\scriptstyle\text{model}}(x)$ without explicitly defining it.
- Why Generative Models?
Realistic samples for artwork, super-resolution, colorization, etc.
Learn useful features for downstream tasks such as classification.
Getting insights from high-dimensional data (physics, medical imaging, etc.)
Modeling physical world for simulation and planning (robotics and reinforcement learning applications)
…
PixelRNN and PixelCNN; a brief overview
- Fully visible belief network (FVBN)
is an explicit density model, defines tractable density function using chain rule to decompose the likelihood of an image x into product of 1-d distributions:
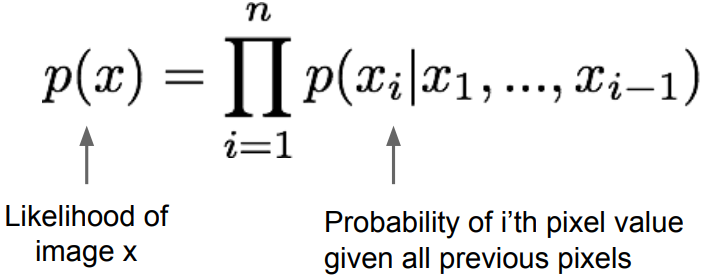
Then maximize likelihood of training data. It is a complex distribution over pixel values, express using a neural network.
PixelRNN, van der Oord et al., 2016
- Generate image pixels starting from corner, dependency on previous pixels modeled using an RNN(LSTM).
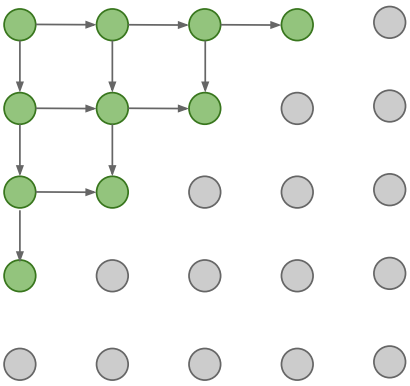
Drawback: sequential generation is slow in both training and inference
PixelCNN, van der Oord et al., 2016
-
Generate image pixels starting from corner, ependency on previous pixels modeled using a CNN over context region(masked convolution)
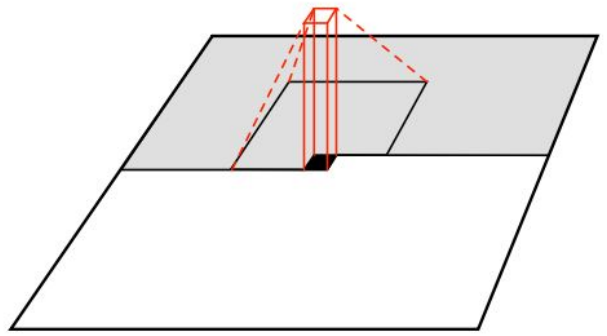
Training is faster than PixelRNN: it can parallelize convolutions since context region values known from training images.
Generation is still slow: for a 32x32 image, we need to do forward passes of the network 1024 times for a single image. -
Improving PixelCNN performance
Gated convolutional layers, Short-cut connections, Discretized logistic loss, Multi-scale, Training tricks, etc.
See also PixelCNN++, Salimans et al., 2017
Summary
- Pros:
Can explicitly compute likelihood p(x)
Easy to optimize
Good samples - Cons:
Sequential generation is slow
Variational Autoencoder(VAE)
- VAE is an explicit density model, defines intractable(approximate) density function with latent z:
$p_\theta(x) = \int p_\theta(z)p_\theta(x|z)\, dz$
No dependencies among pixels, can generate all pixels at the same time. But cannot optimize directly, derive and optimize lower bound on likelihood instead
Background: Autoencoders
- Unsupervised approach for learning a lower-dimensional feature representation from unlabeled training data
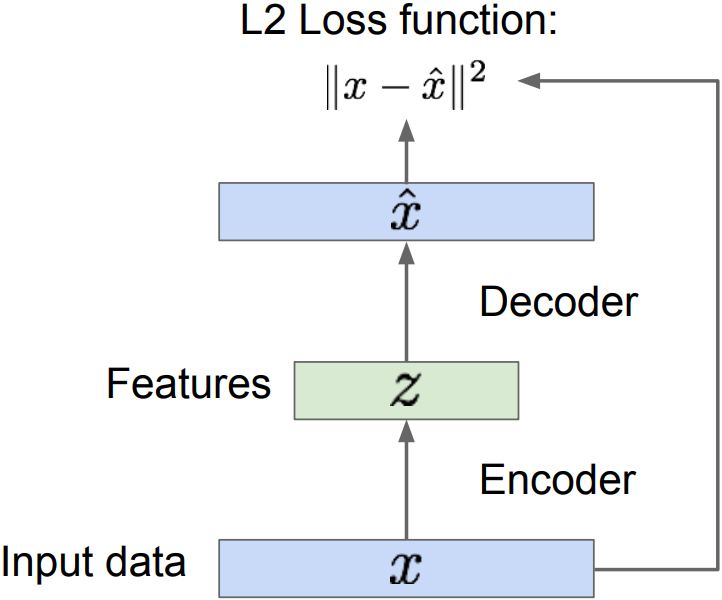
- z usually smaller than x: with dimensionality reduction to capture meaningful factors of variation in data. Train such that features can be used to reconstruct original data($\hat{x}$)
- “Autoencoding”; encoding input itself(L2 loss)
- After training, throw away decoder and adjust to the final task
-
Encoder can be used to initialize a supervised model; Transfer from large, unlabeled dataset(Autoencoder) to small, labeled dataset and fine-tune; train for final task.
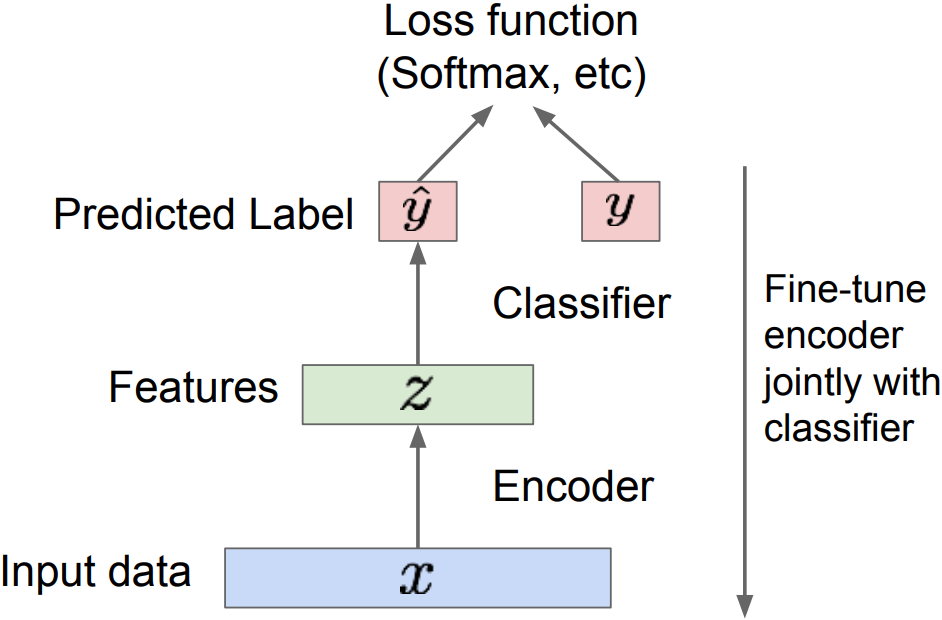
- But we can’t generate new images from an autoencoder because we don’t know the space of z. $\rightarrow$ Variational Autoencoders for a generative model.
Variational Autoencoders: Probabilistic spin on autoencoders
- Assume training data \(\left\{ x^{(i)}\right\} _{i=1}^N\) is generated from the distribution of unobserved (latent) representation z
- Intuition from autoencoders: x is an image, z is latent factors used to generate x: attributes, orientation, etc.
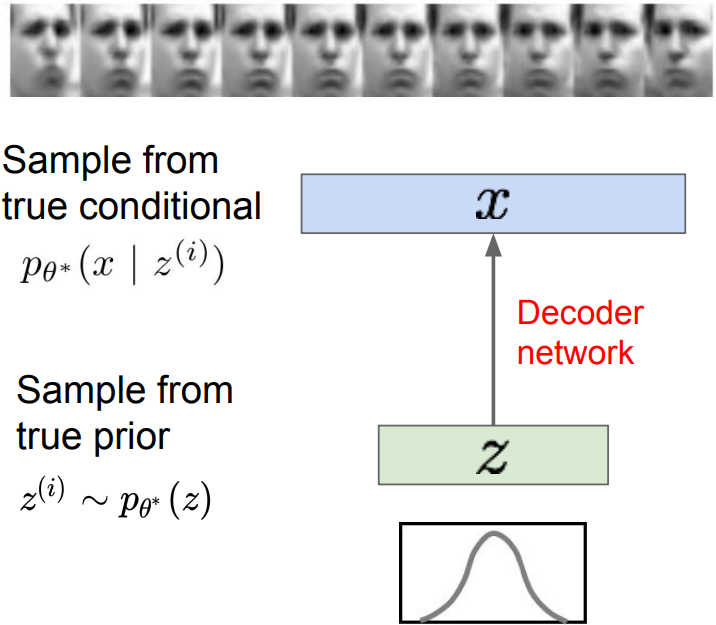
- We want to estimate the true parameters $\theta^*$ of this generative model given training data x.
- Model representation:
- p(z): Choose prior to be simple, e.g. Gaussian.
- z: Reasonable for latent attributes, e.g. pose, how much smile.
- p(x|z): Generating images, conditional probability is complex
$\rightarrow$ represent with neural network - $p_\theta(x)$: Learn model parameters to maximize likelihood of training data
Variational Autoencoders: Intractability
- Data likelihood:
$p_\theta(x) = \int p_\theta(z)p_\theta(x|z)\, dz$
where $p_\theta(z)$ is a Simple Gaussian prior and $p_\theta(x|z)$ is a decoder neural network, it is intractable to compute p(x|z) for every z.
while Monte Carlo estimation-$\log p(x) \approx \log\frac{1}{k}\sum_{i=1}^k p(x|z^{(i)})$, where $z^{(i)}\sim p(z)$- is too high variance. - divided by intractable $p_\theta(x)$, Posterior density also intractable:
$p_\theta(z|x) = p_\theta(x|z)p_\theta(z)/p_\theta(x)$ - Solution:
In addition to modeling $p_\theta(x|z)$, learn $q_\phi(z|x)$ that approximates the true posterior $p_\theta(z|x)$. $q_\phi$, approximate posterior allows us to derive a lower bound on the data likelihood that is tractable, which can be optimized.
Variational inference is to approximate the unknown posterior distribution from only the observed data x
- With taking expectation with respect to z(using encoder network) let us write nice KL terms;
- \(\mathbf{E}_z \left[\log p_\theta(x^{(i)}\vert z) \right]\): Decoder network gives $p_\theta(x\vert z)$, can compute estimate of this term through sampling(need some trick to differentiate through sampling). It reconstruct the input data.
- \(D_{KL}(q_\phi(z\vert x^{(i)})\vert p_\theta(z))\): KL term between Gaussian for encoder and z prior has nice closed-form solution. Encoder makes approximate posterior distribution close to prior.
- \(D_{KL}(q_\phi(z\vert x^{(i)})\vert p_\theta(z\vert x^{(i)}))\): is intractable, we can’t compute this term; but we know KL divergence always greater than 0.
-
To maximize the data likelihood, we can rewrite
\(\begin{align*} \log p_\theta (x^{(i)}) &= \mathbf{E}_z \left[ \log p _\theta (x^{(i)}\vert z) \right] - D_{KL}(q_\phi (z\vert x^{(i)})\vert p_\theta (z)) + D_{KL}(q_\phi (z\vert x^{(i)})\vert p_\theta (z\vert x^{(i)})) \\ &= \mathcal{L}(x^{(i)},\theta ,\phi ) + (C\ge 0) \end{align*}\) - \(\mathcal{L}(x^{(i)},\theta,\phi)\): Decoder - Encoder
Tractable lower bound which we can take gradient of and optimize. Maximizing this evidence lower bound(ELBO), we can maximize $\log p_\theta(x)$. Later, we take minus on this term for the loss function of a neural network.
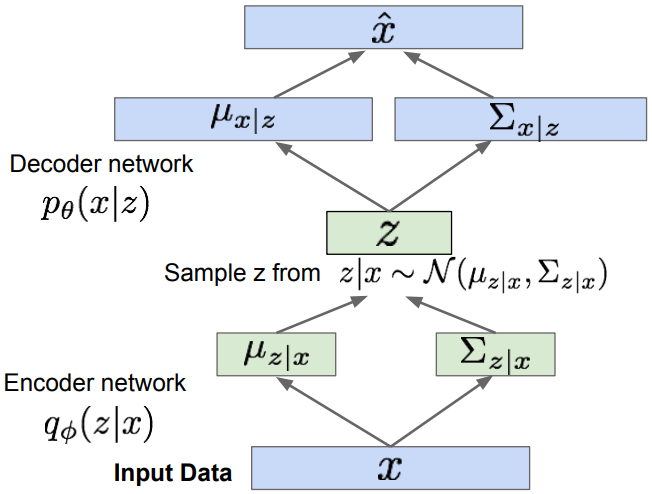
- Encoder part; \(D_{KL}(q_\phi(z\vert x^{(i)})\vert p_\theta(z))\)
We choose q(z) as a Gaussian distribution, $q(z\vert x) = N(\mu_{z\vert x}, \Sigma_{z\vert x})$. Computing the KL divergence, \(D_{KL}(N(\mu_{z\vert x}, \Sigma_{z\vert x}))\vert N(0,I))\), having analytical solution. - Reparameterization trick z:
to make sampling differentiable, input sample $\epsilon\sim N(0,I)$ to the graph $z = \mu_{z\vert x} + \epsilon\sigma_{z\vert x}$; where $\mu, \sigma$ are the part of computation graph. - Decoder part;
Maximize likelihood of original input being reconstructed, $\hat{x}-x$. - For every minibatch of input data, compute $\mathcal{L}$ graph forward pass and backprop.
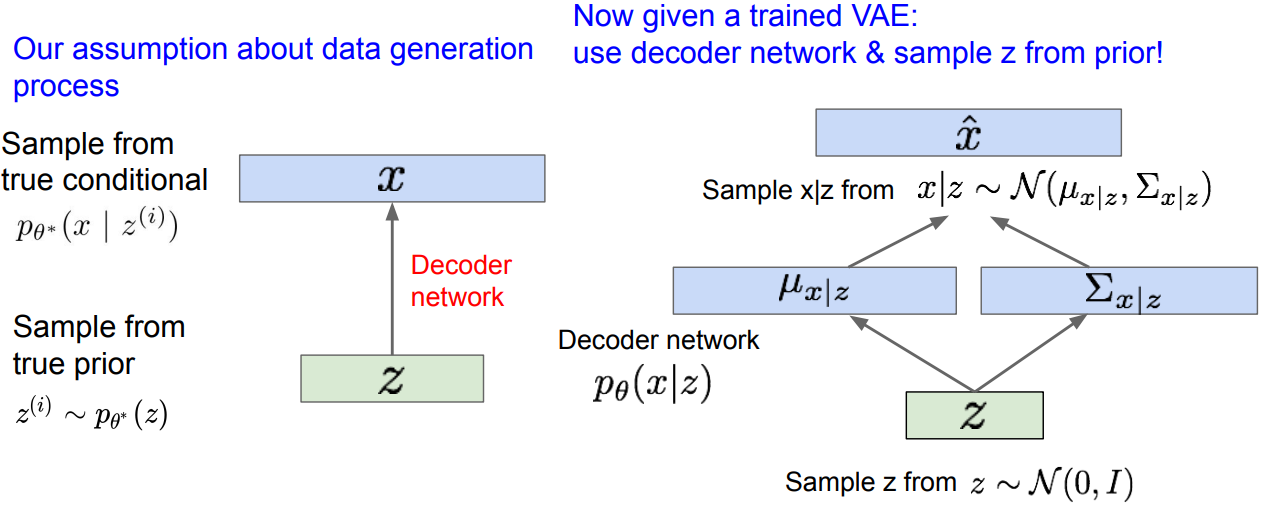
Variational Autoencoders: Generating Data
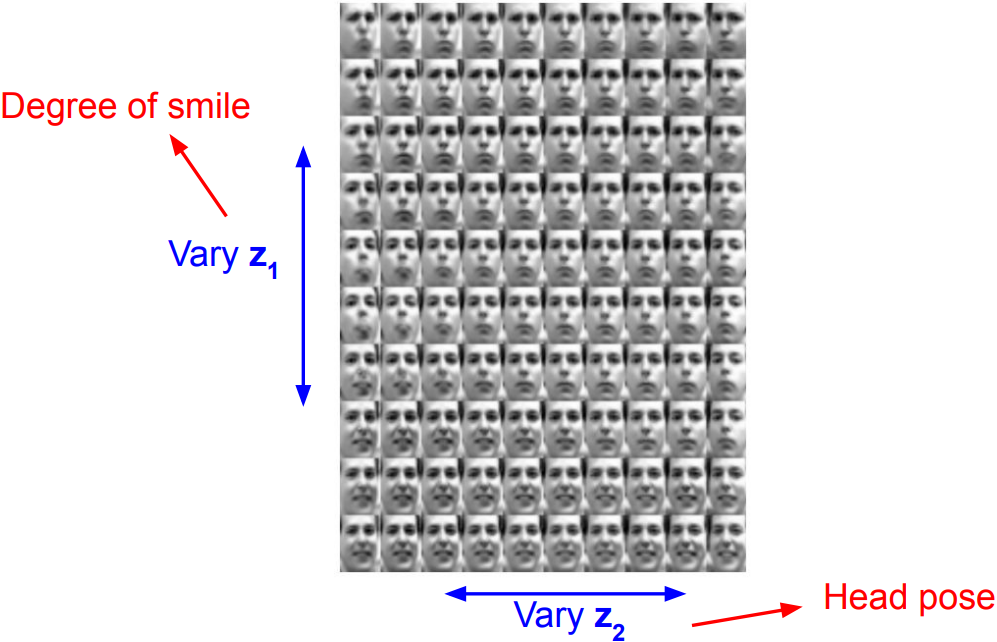
- Diagonal prior on z for independent latent variables
- Different dimensions of z encode interpretable factors of variation;
Also good feature representation taht can be computed using $q_\phi(z\vert x)$.
Summary
- Probabilistic spin to traditional autoencoders, allows generating data
-
Defines an intractable density; derive and optimize a (variational) lower bound
- Pros:
Principled approach to generative models
Interpretable latent space
Allows inference of $q(z\vert x)$, can be useful feature representation for other tasks - Cons:
Maximizes lower bound of likelihood: not as good evaluation as tractable model
Samples mean; blurrier and lower quality compared to state-of-the-art (GANs)
Generative Adversarial Networks(GANs)
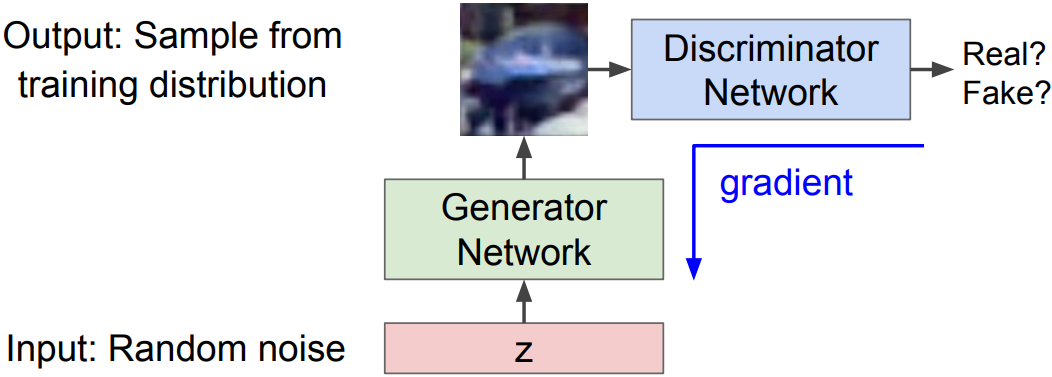
idea: Use a discriminator network to tell whether the generate image is within data distribution (“real”) or not
Training GANs: Two-player game
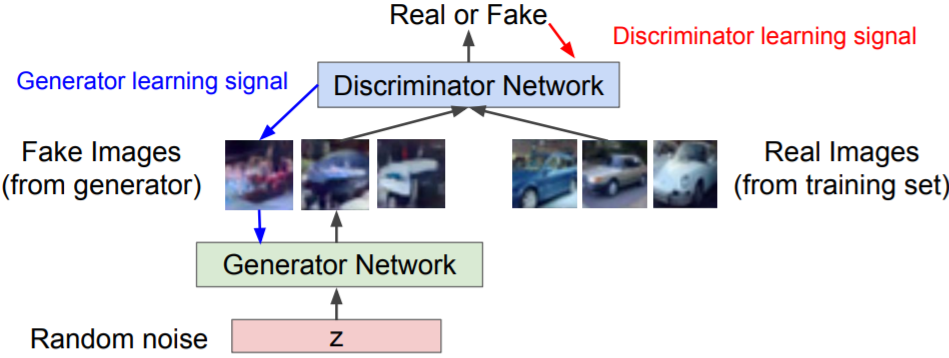
Discriminator network: try to distinguish between real and fake images
Generator network: try to fool discriminator by generating real-looking images
- Train jointly in minimax game;
Minimax objective function:
\(\mbox{min}_{\theta_g} \mbox{max}_{\theta_d}\left[\mathbb{E}_{x\sim {p_{data}}}\log D_{\theta_d}(x) + \mathbb{E}_{z\sim p(z)}\log(1-D_{\theta_d}(G_{\theta_g}(z))) \right]\)
where $\theta_g$ is an objective for the generator objective and $\theta_d$ for the discriminator- $D_{\theta_d}(x)$: Discriminator outputs likelihood in (0,1) of real image
- $D_{\theta_d}(G_{\theta_g}(z))$: Discriminator output for generated fake data G(z)
- Discriminator($\theta_d$) wants to maximize objective such that D(x) is close to 1(real) and D(G(z)) is close to 0(fake)
- Generator($\theta_g$) wants to minimize objective such that D(G(z)) is close to 1(to fool discriminator)
We alternate the minimax objection function with:
- Gradient ascent on discriminator
\(\mbox{max}_{\theta_d}\left[\mathbb{E}_{x\sim p_{data}}\log D_{\theta_d}(x) + \mathbb{E}_{z\sim p(z)}\log(1-D_{\theta_d}(G_{\theta_g}(z))) \right]\) - 1) Gradient descent on generator
\(\mbox{min}_{\theta_g}\mathbb{E}_{z\sim p(z)}\log(1-D_{\theta_d}(G_{\theta_g}(z)))\)- In practice, optimizing this generator objective does not work well;
When sample is likely fake, want to learn from it to improve generator (move to the right on X axis), but gradient near 0 in X axis is relatively flat; Gradient signal is dominated by region where sample is already good(near 1).
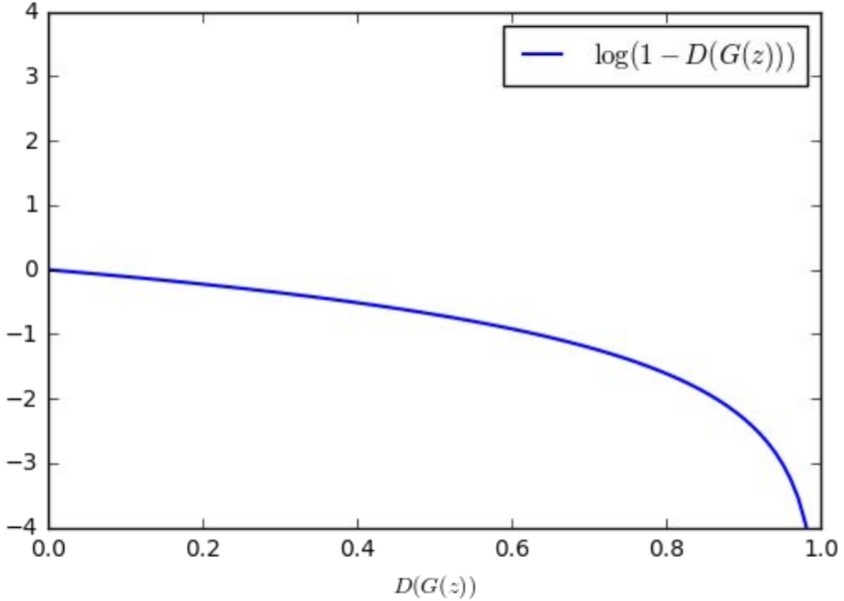
2) Instead: Gradient ascent on generator, different objective
\(\mbox{max}_{\theta_d}\mathbb{E}_{z\sim p(z)}\log(D_{\theta_d}(G_{\theta_g}(z)))\)- Rather than minimizing likelihood of discriminator being correct, maximize likelihood of discriminator being wrong. Same objective of fooling discriminator, but now higher gradient signal for bad samples.
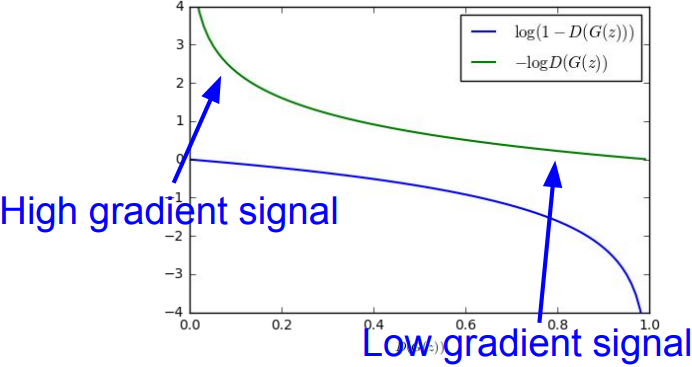
- In practice, optimizing this generator objective does not work well;
-
GAN training Algorithm

-
After training, use generator network to generate new images
GAN: Convolutional Architectures
-
Generator is an upsampling network with fractionally-strided convolutions
Discriminator is a convolutional network -
Architecture guidelines for stable Deep Conv GANs
- Replace any pooling layers with strided convolutions(discriminator) and fractional-strided convolutions(generator).
- Use batchnorm in both network.
- Remove fully connected hidden layers for deeper architecture.
- Use ReLU activation in generator for all layers except for the output, which uses Tanh.
- Use LeakyReLU activation in the discriminator for all layers.
GAN: Interpretable Vector Math
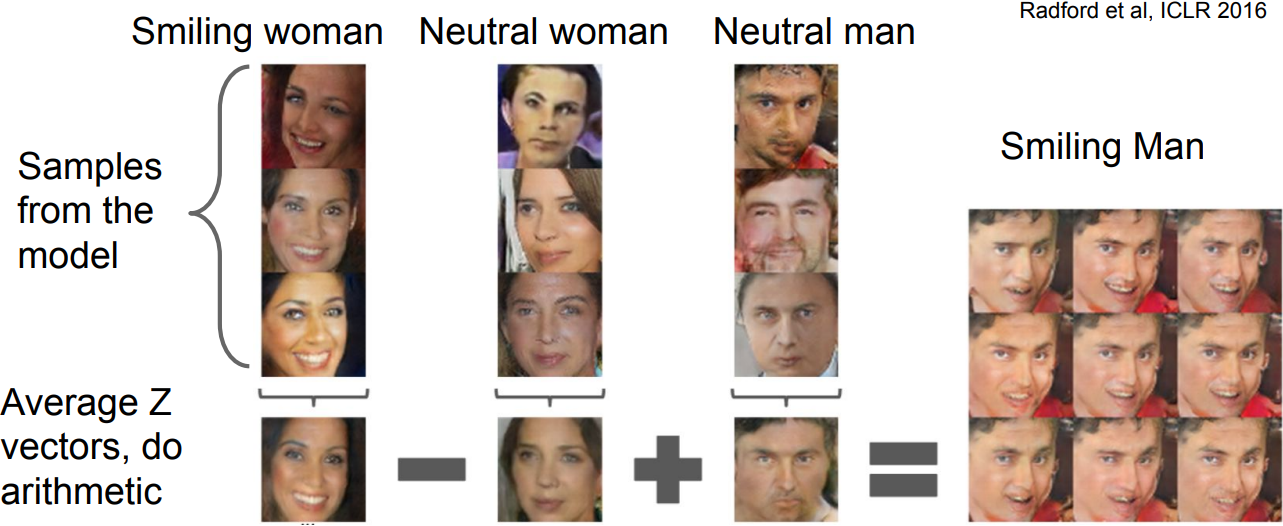
- works similar to a language model
2017: Explosion of GANs
- “The GAN Zoo”,
https://github.com/hindupuravinash/the-gan-zoo - check
https://github.com/soumith/ganhacksfor tips and tricks for training GANs
Scene graphs to GANs
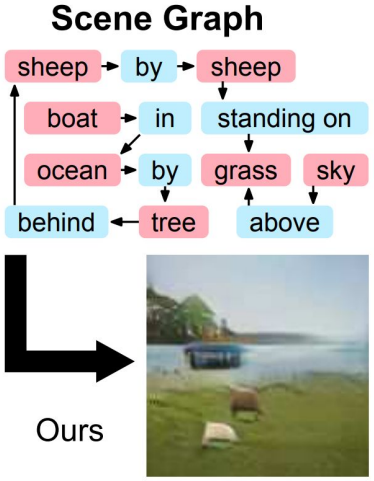
- Specifying exactly what kind of image you want to generate. The explicit structure in scene graphs provides better image generation for complex scenes.
Summary: GANs
- Don’t work with an explicit density function
-
Take game-theoretic approach: learn to generate from training distribution through 2-player game
- Pros:
- Beautiful, state-of-the-art samples
- Cons:
- Trickier / more unstable to train
- Can’t solve inference queries such as $p(x)$, $p(z\vert x)$
- Active areas of research:
- Better loss functions, more stable training (Wasserstein GAN, LSGAN, many others)
- Conditional GANs, GANs for all kinds of applications
- Useful Resources on Generative Models
CS236: Deep Generative Models (Stanford)
CS 294-158 Deep Unsupervised Learning (Berkeley)