Convolutional Neural Networks

• ConvNets are everywhere
  Classification, Retrieval, Detection, Segmentation, Image Captioning, etc.

• Recap: Fully Connected Layer
  $32\times 32\times 3$ image $\rightarrow$ stretch to $3072\times 1$
  Then a dot product of $3072\times 1$ input x and scoring weights W, Wx is in $10 \times 3072$. With some activation function, we can make classification scores in 10 classes.

Convolution Layer: preserve spatial structure

• Convolve the filter with the image, slide over the image spatially, computing dot products. Filters always extend the full depth of the input volume.
  
  Convolve(slide) over all spatial locations, we can make an activation map of size $28\times 28\times 1$ for each convolution filter. For example, if we had 6 $5\times 5$ filters, we’ll get 6 separate activation maps. We stack these up to get a “new image” of size $28\times 28\times 6$.

• ConvNet is a sequence of Convolution Layers, interspersed with activation functions.
  
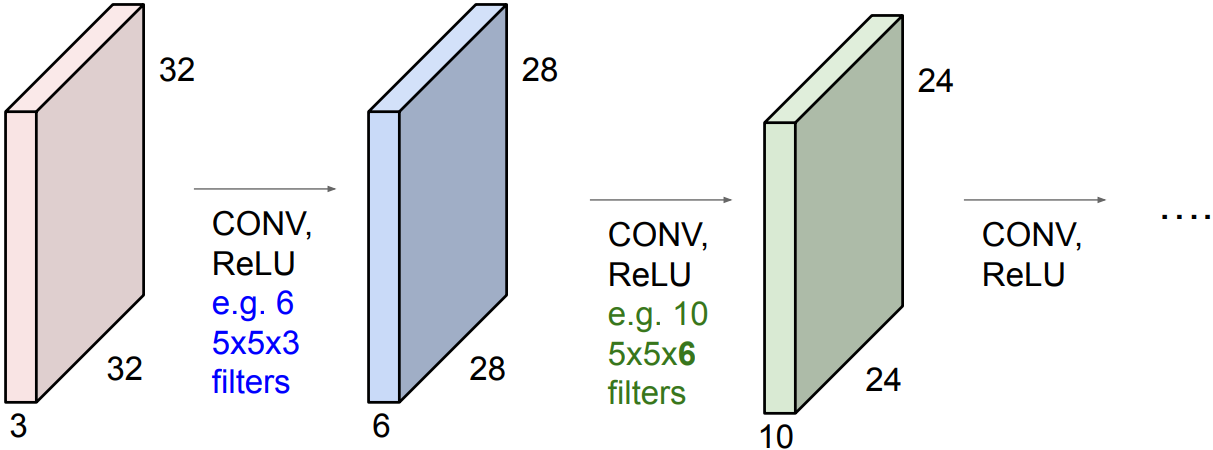
  Input convolved repeatedly with filters shrinks volumes spatially. By each sequence, an image is processed from low-level features to high-level features. Shrinking too fast is not good, doesn’t work well.

• We call the layer convolutional because it is related to convolution of two signals: \(f[x,y]*g[x,y]=\sum_{n_1=-\infty}^\infty \sum_{n_2=-\infty}^\infty f[n_1,n_2]\cdot g[x-n_1,y-n_2]\); elementwise multiplication and sum of a filter and the signal (image)

• Zero pad the border:
  The data on the border of an image will be convolved only once with each filter, while the others on the center of an image will be treated several times. Zero padding is introduced to solve this problem.

• General CONV layers:
  with $N\times N$ input, $F\times F$ filter, applied with stride s, pad with p pixel border, the output is $(N+2P-F)/s + 1$

• Example:
  Input volume $32\times 32\times 3$
  10 $5\times 5$ filters with stride 1, pad 2

  $\rightarrow$ Output volume size: $(32+2*2-5)/1+1=32$ spatially, so $32\times 32\times 10$.

  $\rightarrow$ Number of parameters in this layer: each filter has $5\times 5\times 3+1=76$ parameters(+1 for bias), thus for all 760 params.

• $1\times 1$ convolution layers used:
  To reduce the number of channels, so the number of parameters,
  Then we can perform a deeper layers(Bottleneck architecture).

Pooling layer

• Summarize the data in a partial space, into some representations
  Reducing output dimensions and the number of parameters
  Make it smaller and more manageable
  Operate over each activation map independently(downsampling)

• e.g. max pool with $2\times 2$ filters and stride 2, $4\times 4$ input reduced to $2\times 2$ output consisted of regional maximums.

Fully Connected Layer (FC layer)

• Contains neurons that connect to the entire input volume, as in ordinary Neural Networks. Stacked and followed by some activations, finally we make predictions or classifications.

Summary

• ConvNets stack CONV,POOL,FC layers
• Trend towards smaller filters and deeper architectures
• Trend towards getting rid of POOL/FC layers (just CONV)
• Historically architectures looked like [(CONV-RELU)*N-POOL?]*M-(FC-RELU)*K,SOFTMAX where N is usually up to ~5, M is large, $0\le K \le 2$.
• but recent advances such as ResNet/GoogLeNet have challenged this paradigm