/ CS224N

cs224n - Lecture 5. Language Models and RNNs

How do we gain from a neural dependency parser?

  • So far…
    Transition based dependency parsers were an efficient linear time method for giving the syntactic structure of natural language text.
    Worked pretty well before neural nets came along.
    $\color{red}{(-)}$ They worked with indicator features, specifying some condition and then checking whether it was true of a configuration. Problems of those features are:
    • Problem #1: sparse
    • Problem #2: incomplete
    • Problem #3: expensive computation
      More than 95% of parsing time is consumed by feature computation
  • Neural Approach:
    Start with the same configuration of a stack and a buffer, run exactly the same transition sequence but with a dense vector.

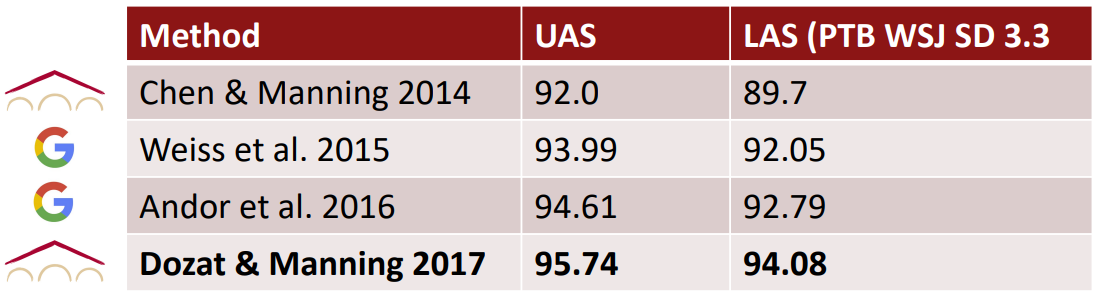
A neural dependency parser(Chen and Manning, 2014)

png

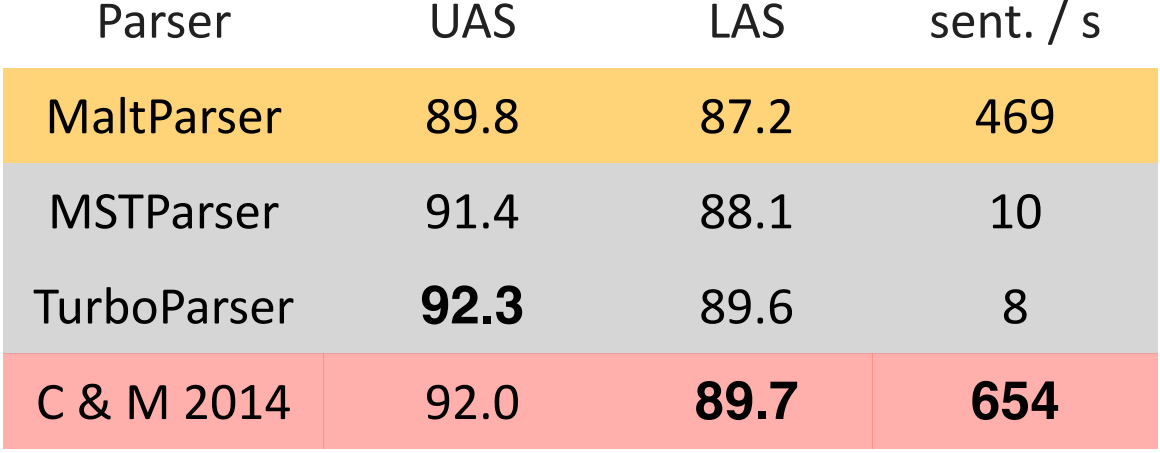
  • Results on English parsing to Stanford Dependencies:
    • Unlabeled attachment score (UAS) = head
    • Labeled attachment score (LAS) = head and label
    • 2% more accurate than the symbolic dependency parser
    • noticeably faster

First win: Distributed Representations

  • Represent each word as a d-dimensional dense vector (i.e., word embedding)
    • Similar words are expected to have close vectors.
  • Meanwhile, part-of-speech tags(POS) and dependency labels are also represented as d-dimensional vectors.
    • The smaller discrete sets also exhibit many semantical similarities.
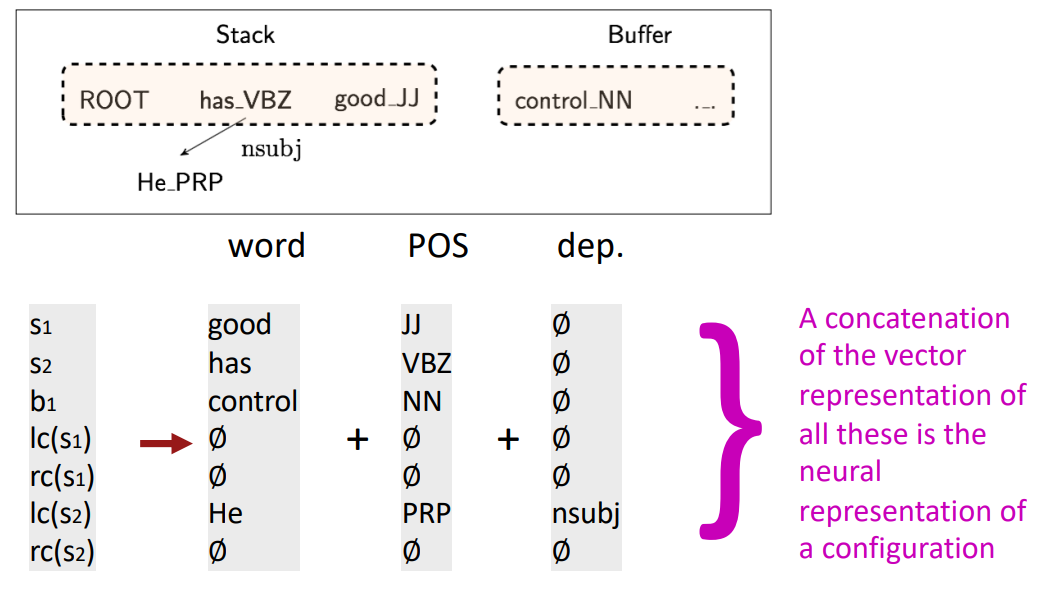
  • Extracting Tokens & vector representations from configuration
    • Extract a set of tokens based on the stack / buffer positions:

png

Second win: Deep Learning classifiers are non-linear classifiers

  • A softmax classifier assigns classes $y\in C$ based on inputs $x \in \mathbb{R}^d$ via the probability:
    \(\begin{align*} p(y\mid x) = \frac{\exp(W_y . x)}{\sum_{c=1}^C \exp(W_c . x)} \end{align*}\)

  • We train the weight matrix $W \in \mathbb{R}^{C\times d}$ to minimize the neg. log loss: $\sum_i - \log p(y_i\mid x_i)$ (a.k.a. “cross entropy loss”)

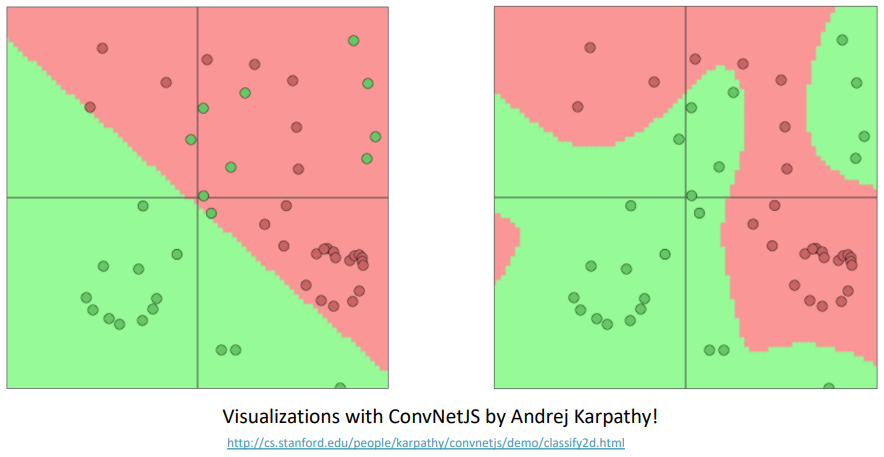
  • Traditional ML classifiers (including Naive Bayes, SVMs, logistic regression and softmax classifier) are not very powerful classifiers: they only give linear decision boundaries; limiting, unhelpful when a problem is complex.

  • Neural networks can learn much more complex functions with nonlinear decision boundaries.
    • Non-linear in the original space, linear for the softmax at the top of the neural network

png

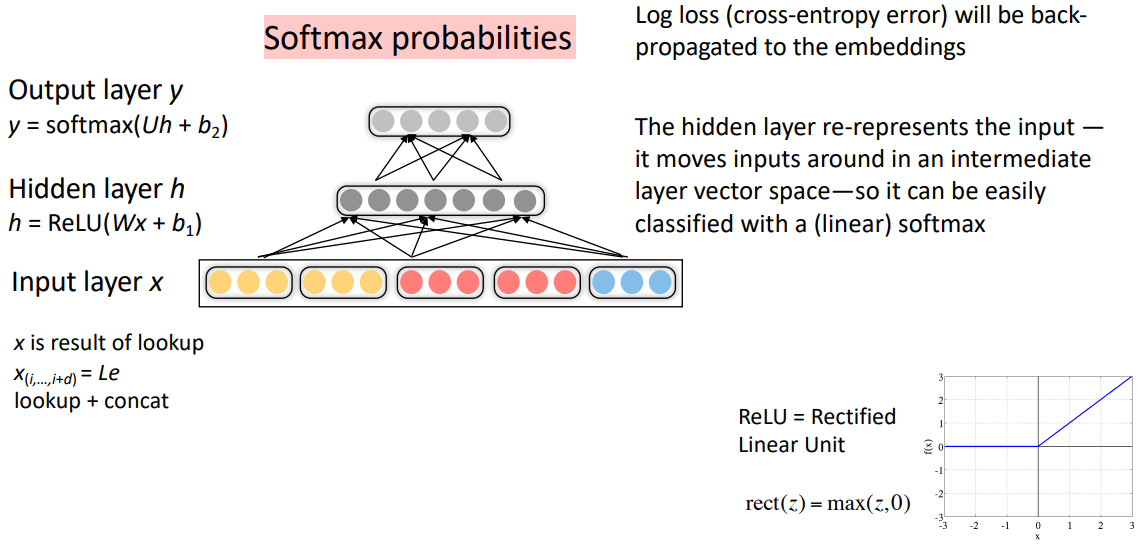
Simple feed-forward neural network multi-class classifier

png

Neural Dependency Parser Model Architecture

png

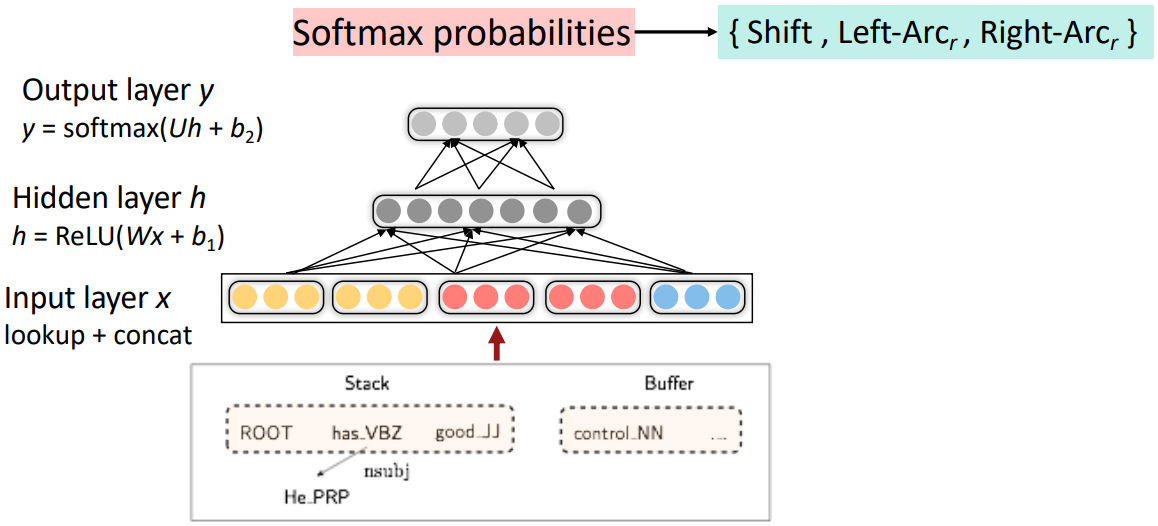
Dependency parsing for sentence structure

  • C & M 2014 showed that neural networks can accurately determine the structure of sentences, supporting meaning interpretation

png

  • It was the first simple, successful neural dependency parser
  • The dense representations (and non-linear classifier) let it outperform other greedy parsers in both accuracy and speed

Further developments in transition-based neural dependency parsing

Graph-based dependency parsers

  • Compute a score for every possible pair; dependency (choice of head) for each word
    • Doing this well requires more than just knowing the two words
    • We need good “contextual” representations of each word token, which we will develop in the coming lectures
  • Repeat the same process for each other word; find the best parse (MST algorithm)

png

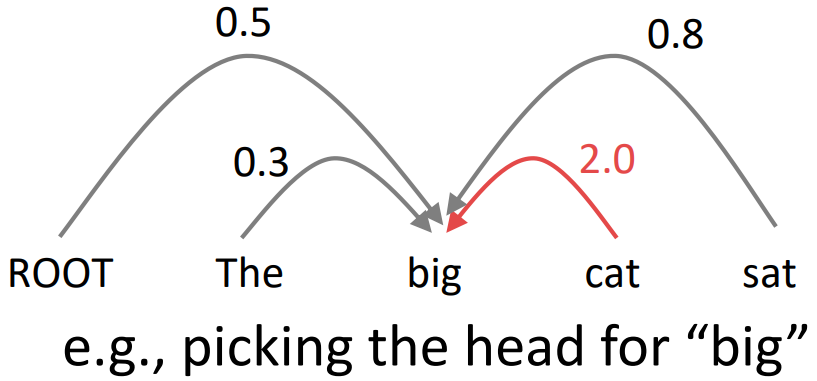
A Neural graph-based dependency parser

  • Dozat and Manning 2017; Dozat, Qi, and Manning 2017

  • This paper revived interest in graph-based dependency parsing in a neural world
    • Designed a biaffine scoring model for neural dependency parsing
    • Also crucially uses a neural sequence model
  • Great results, but slower than the simple neural transition-based parsers
    • There are $n^2$ possible dependencies in a sentence of length $n$

png

A bit more about neural networks

Regularization

  • A full loss function includes regularization over all parameters $\theta$, e.g., L2 regularization:
    \(\begin{align*} J(\theta) = \frac{1}{N}\sum_{i=1}^N -\log \left( \frac{e^{f_{y_i}}}{\sum_{c=1}^C e^{f_c}} \right) + \lambda\sum_k \theta_k^2 \end{align*}\)

  • Classic view: Regularization works to prevent overfitting when we have a lot of features (or later a very powerful/deep model, etc.)

  • Now: Regularization produces models that generalize well when we have a “big” model

    • We do not care that our models overfit on the training data, even though they are hugely overfit

Dropout

  • [Srivastava, Hinton, Krizhevsky, Sutskever, & Salakhutdinov 2012/JMLR 2014]

  • Preventing Feature Co-adaptation = Good Regularization Method

    • Training time: at each instance(or batch) of evaluation (in online SGD-training), randomly set 50% of the inputs to each neuron to 0
    • Test time: halve the model weights (because we now keep twice as many active neurons)
      (Except usually only drop first layer inputs a little (~15%) or not at all)
    • Prevents feature co-adaptation: A feature cannot only be useful in the presence of particular other features
    • In a single layer: A kind of middle-ground between Naive Bayes (where all feature weights are set independently) and logistic regression models (where weights are set in the context of all others)
    • Can be thought of as a form of model bagging (i.e., like an ensemble model)
    • Nowadays usually thought of as strong, feature-dependent regularizer
      [Wager, Wang, & Liang 2013]

“Vectorization”

  • E.g., looping over word vectors versus concatenating them all into one large matrix and then multiplying the softmax weights with that matrix:
from numpy import random
N = 500 # number of windows to classify
d = 300 # dimensionality of each window
C = 5 # number of classes
W = random.rand(C, d)
wordvectors_list = [random.rand(d, 1) for i in range(N)]
wordvectors_one_matrix = random.rand(d, N)

%timeit [W.dot(wordvectors_list[i]) for i in range(N)]
%timeit W.dot(wordvectors_one_matrix)
  • Always try to use vectors and matrices rather than for loops; the speed gain goes from 1 to 2 orders of magnitude with GPUs.

Non-linearities, old and new

  • logistic(“sigmoid”)
    \(\begin{align*} f(z) = \frac{1}{1+\exp(-z)}\end{align*}\)
  • tanh
    \(\begin{align*} f(z) = \tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}\end{align*}\)
    tanh is just a rescaled and shifted sigmoid(2x as steep, [-1, 1]):
    $tanh(z) = 2 \text{logistic}(2z) - 1$
  • hard tanh
    \(\begin{align*} \text{PHardTanh}(x) = \begin{cases} -1 & \mbox{ if } x < -1 \\ x & \mbox{ if } -1 \le x \le 1 \\ 1 & \mbox{ if } x > 1 \end{cases}\end{align*}\)

  • ReLU(Rectrified Linear Unit)
    $\text{rect}(z) = \text{max}(z, 0)$

  • Others
    Leaky ReLU / Parametric ReLU, Swish(Ramachandran, Zoph & Le 2017)

  • Both logistic and tanh are still used in various places(e.g., to get a probability), but are no longer the defaults for making deep networks
    For building a deep network, first try ReLU - it trains quickly and performs well due to good gradient backflow

Parameter Initialization

  • Initialize weights to small random values (i.e., not zero matrices)
    To avoid symmetries that prevent learning/specialization
  • Initialize hidden layer biases to 0 and output (or reconstruction) biases to optimal value if weights were 0 (e.g., mean target or inverse sigmoid of mean target)
  • Initialize all other weights $~ \text{Uniform}(–r, r)$, with $r$ chosen so numbers get neither too big or too small (later the need for this is removed with use of layer normalization)
  • Xavier initialization has variance inversely proportional to fan-in $n_{in}$ (previous layer size) and fan-out $n_{out}$ (next layer size):
    \(\begin{align*} Var(W_i) = \frac{2}{n_{in} + n_{out}} \end{align*}\)

Optimizers

  • SGD will work just fine, but getting good results will often require hand-tuning the learning rate
  • Sophisticated “adaptive” optimizers that scale the parameter adjustment by an accumulated gradient; Adam is fairly good, safe place to start in many cases

Learning Rates

  • A constant learning rate. Start around $lr = 0.001$?
    • It must be order of magnitude right – try powers of 10
      Too big: model may diverge or not converge
      Too small: model may not have trained by the assignment deadline
  • Better try learning rate decay
    • By hand: : halve the learning rate every k epochs
    • By a formula: $lr = lr_0 e^{-kt}$, for epoch $t$
    • There are fancier methods like cyclic learning rates (q.v.)
  • Fancier optimizers still use a learning rate but it may be an initial rate that the optimizer shrinks – so you may want to start with a higher learning rate

Language Modeling

  • Language Modeling is the task of predicting what word comes next

  • More formally: given a sequence of words $x^{(1)}, x^{(2)}, \ldots, x^{(t)}$, compute the probability distribution of the next words $x^{(t+1)}$:
    $P(x^{(t+1)} \mid x^{(t)}, \ldots, x^{(1)})$
    where $x^{(t+1)}$ can be any word in the vocabulary \(V = \left\{ w_1, \ldots, w_{\lvert V \rvert} \right\}\)

  • You can also think of a Language Model as a system that assigns probability to a piece of text

  • For example, if we have some text $x^{(1)}, x^{(2)}, \ldots, x^{(T)}$, then the probability of this text (according to the Language Model) is:
    \(\begin{align*} P(x^{(1)}, \ldots, x^{(T)}) &= P(x^{(1)}) \times P(x^{(2)}\mid x^{(1)}) \times \cdots \times P(x^{(T)}\mid x^{(T-1)}, \ldots, x^{(1)}) \\ &= \prod_{t=1}^T \underbrace{P(x^{(t)}\mid x^{(t-1)}, \ldots, x^{(1)})}_{\text{This is what our LM provides}} \end{align*}\)

n-gram Language Models

  • Question: How to learn a Language Model?
  • Answer(traditional, pre- Deep Learning): learn an n-gram Language Model
  • Definition: A _n-gram__ is a chunk of n consecutive words.
  • Idea: Collect statistics about how frequent different n-grams are and use these to predict next word.
  • First we make a Markov assumption: $x^{(t+1)}$ depends only on the preceding n-1 words;
\[\begin{align*} P(x^{(t+1)}\mid x^{(t)}, \ldots, x^{(1)}) &= \overbrace{P(x^{(t+1)}\mid x^{(t)}, \ldots, x^{(t-n+2)})}^{n-1 \text{words}} &\text{(assumption)} \\ &= \frac{\overbrace{P(x^{(t+1)}, x^{(t)}, \ldots, x^{(t-n+2)})}^{\text{prob of a n-gram}}}{\underbrace{P(x^{(t)}, \ldots, x^{(t-n+2)})}_{\text{prob of a (n-1)-gram}}} &\text{(definition of conditional prob)} \end{align*}\]
  • Question: How do we get these n-gram and (n-1)-gram probabilities?
  • Answer: By counting them in some large corpus of text
\[\begin{align*} \approx \frac{\text{count}(x^{(t+1)}, x^{(t)}, \ldots, x^{(t-n+2)})}{\text{count}(x^{(t)}, \ldots, x^{(t-n+2)})} &&\text{(statistical approxtimation)} \end{align*}\]

n-gram Language Models: Example

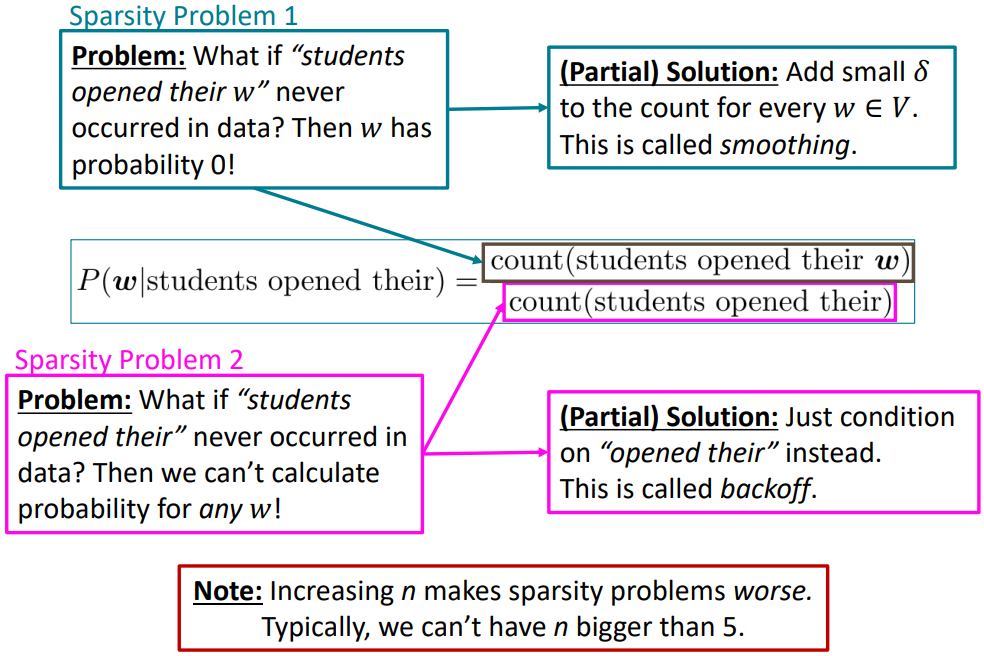
Suppose we are learning a 4-gram Language Model.

as the proctor started the clock, the students opened their w(target)

\(\begin{align*} P(\mathbf{w}|\text{students opened their}) = \frac{\text{count}(\text{students opened their } \mathbf{w})}{\text{students opened their}} \end{align*}\)

  • For example, suppose that in the corpus:
    • “students opened their” occurred 1000 times
    • “students opened their books” occurred 400 times
      $\rightarrow P(\text{books}|\text{students opened their}) = 0.4$
    • “students opened their exams” occurred 100 times
      $\rightarrow P(\text{exams}|\text{students opened their}) = 0.1$
      Then, Should we have discarded the “proctor” context?
  • Naive Bayes: a class specific unigram language model, counting individual words

Problems with n-gram Language Models

  • Sparsity:

png

  • Storage: Need to store count for all n-grams you saw in the corpus
    Increasing n or increasing corpus increases model size

n-gram Language Models in practice

  • You can build a simple trigram Language Model over a 1.7 million word corpus (Reuters) in a few seconds on your laptop

png

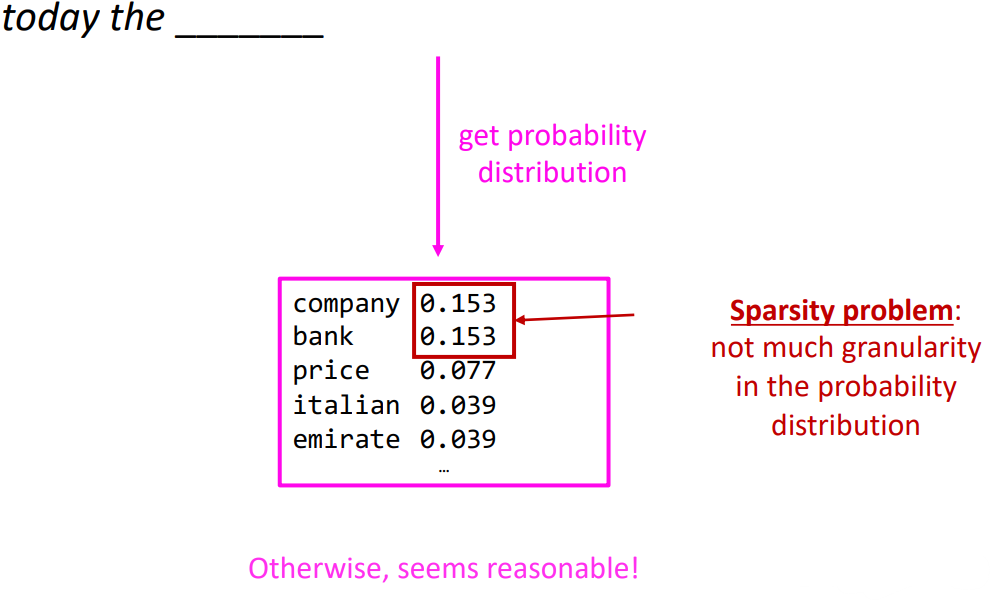
  • You can also use a Language Model to generate text
    • Get probability distribution, sample one. move forward and iterate.
    • Results are incoherent. Need to consider more n words but increasing n worsens sparsity problem, and increases model size

How to build a neural Language Model?

  • Recall the Language Modeling task:
    • Input: sequence of words $x^{(1)}, x^{(2)}, \ldots, x^{(t)}$
    • Output: prob dist of the next word $P(x^{(t+1)} \mid x^{(t)}, \ldots, x^{(1)})$
  • Window-based neural model

png

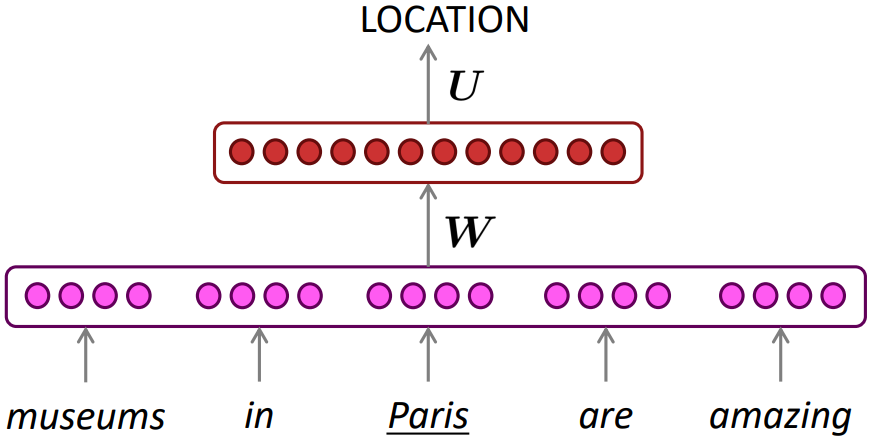
A fixed-window neural Language Model

Approximately: Y. Bengio, et al. (2000/2003): A Neural Probabilistic Language Model
png

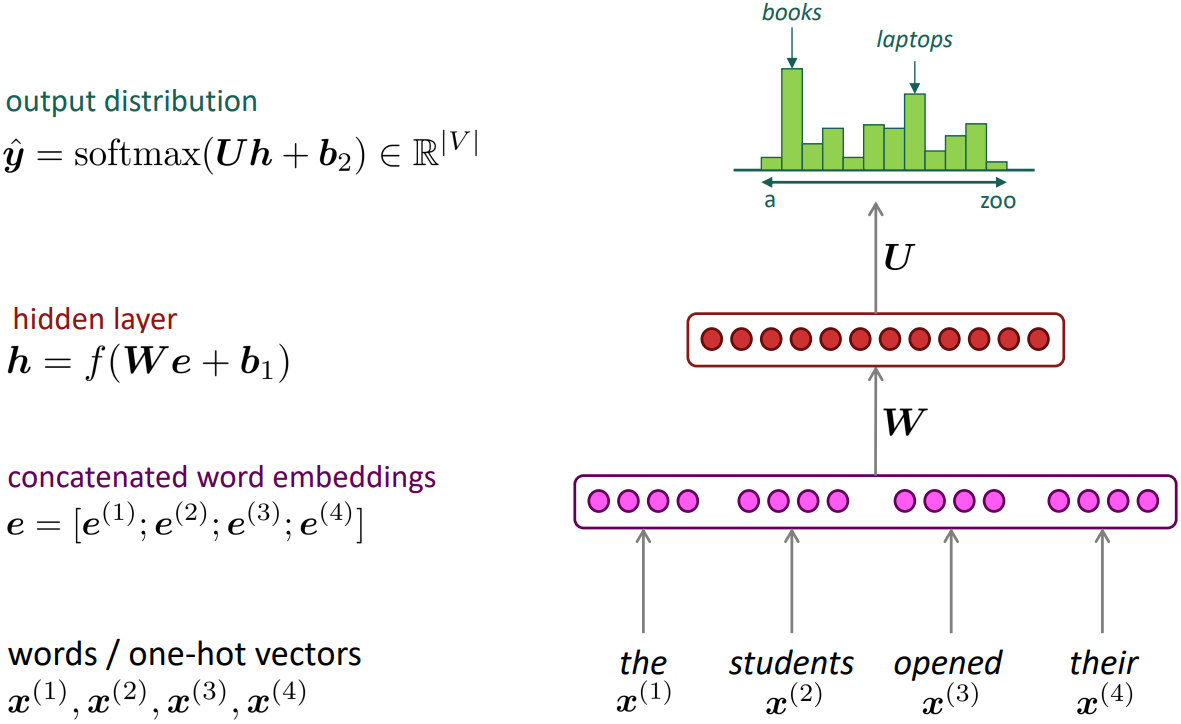
  • Improvements over n-gram LM:
    • No sparsity problem
    • Don’t need to store all observed n-grams
  • Remaining problems:
    • Fixed window is too small
    • Enlarging window enlarges $W$
    • Window can never be large enough
    • $x^{(1)}$ and $x^{(2)}$ are multiplied by completely different weights in $W$. No symmetry in how the inputs are processed.
      $\rightarrow$ We need a neural architecture that can process any length input

Recurrent Neural Networks (RNN)

  • Core idea: Apply the same weights $W$ repeatedly

png
png

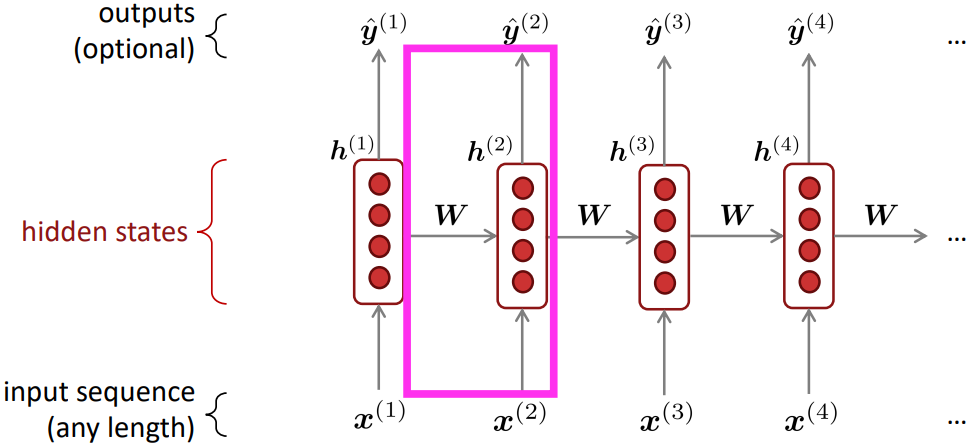
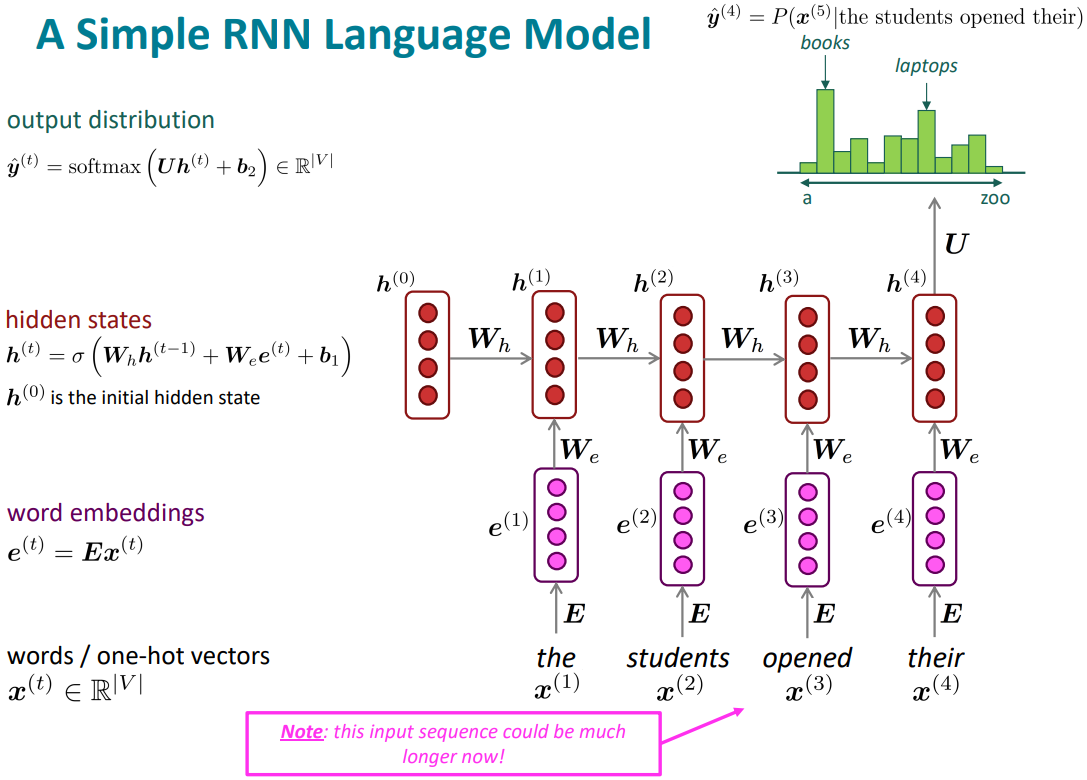
  • RNN Advantages:
    • Can process any length input
    • Computation for step t can (in theory) use information from many steps back
    • Model size doesn’t increase for longer input context
    • Symmetry input process; same weights applied on every timestep
  • RNN Disadvantages:
    • Recurrent computation is slow
    • In practice, difficult to access information from many steps back