RNN: Process Sequences

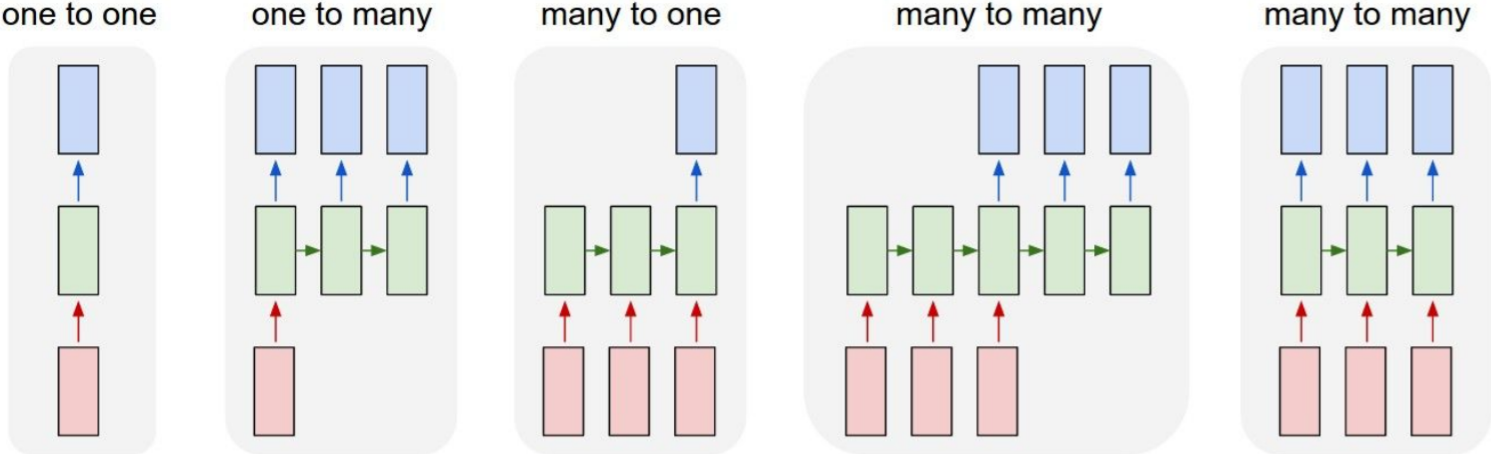
• one to one; vanilla neural networks
• one to many; e.g. Image Captioning(image to sequence of words)
• many to one; e.g. Action Prediction(video sequence to action class)
• many to many(1); e.g. Video Captioning(video sequence to caption)

• many to many(2); e.g. Video Classification on frame level

• Why existing convnets are insufficient?:
  Variable sequence length inputs and outputs

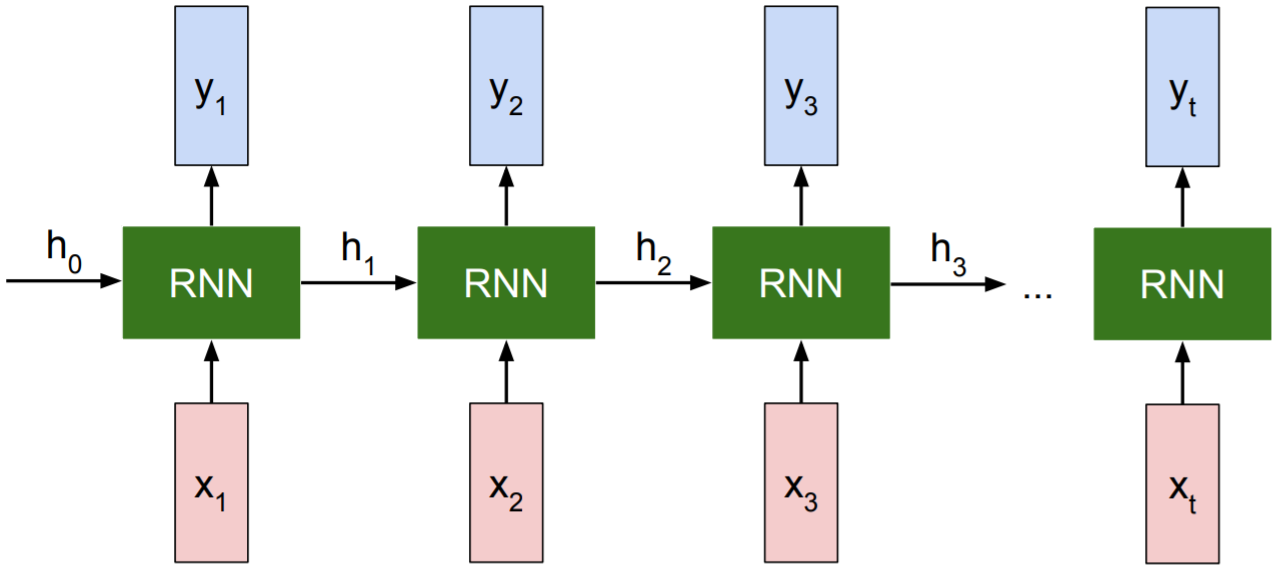
• Key idea: RNNs have an “internal state” that is updated as a sequence is processed.

• RNN hidden state update:
  \(h_t = f_W(h_{t-1}, x_t)\)
  The same function and the same set of parameters are used at every time step.

• RNN output generation: \(y_t = f_{W_hy}(h_t)\)

• Simple(Vanilla) RNN: The state consists of a single hidden vector h
  $h_t = \mbox{tanh}(W_hh h_{t-1} + W_{xh}x_t)$
  $y_t = W_{hy}h_t$

Sequence to Sequence(Seq2Seq): Many-to-One + One-to-Many

• Many-to-One: Encode input sequence in a single vector
  One-to-Many: Produce output sequence from single input vector
  Encoder produces the last hidden state $h_T$ and decoder uses it as a default $h_0$. Weights($W_1, W_2$) are re-used for each procedure.

• Example: Character-level Language Model Sampling

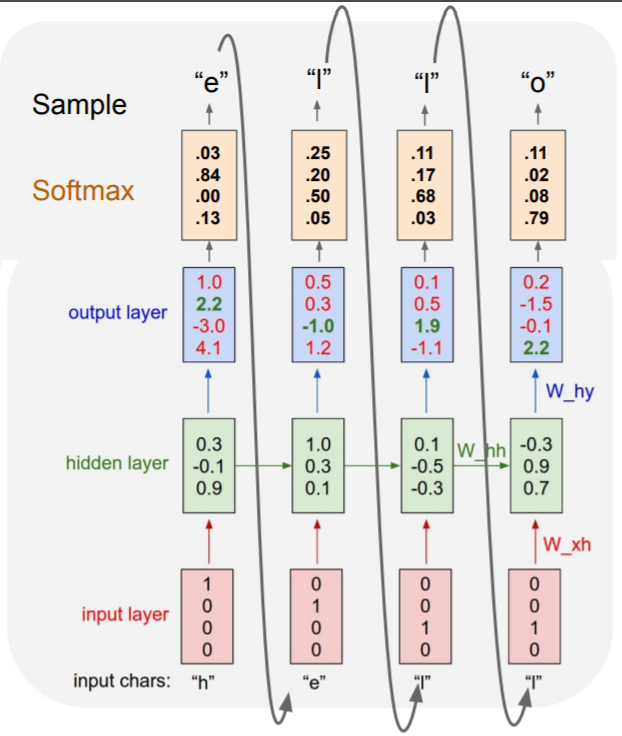
Backpropagation

• Backpropagation through time: Computationally Expensive
  Forward through entire sequence to compute loss, then backward through entire sequence to compute gradient.
• Truncated Backpropagation through time:
  Run forward and backward through chunks of the sequence instead of whole sequence. Carry hidden states forward in time forever, but only backpropagate for some smaller number of steps.

RNN tradeoffs

• RNN Advantages:
  • Can process any length input
  • Computation for step t can (in theory) use information from many steps back
  • Model size doesn’t increase for longer input
  • Same weights applied on every timestep, so there is symmetry in how inputs are processed.
• RNN Disadvantages:
  • Recurrent computation is slow
  • In practice, difficult to access information from many steps back

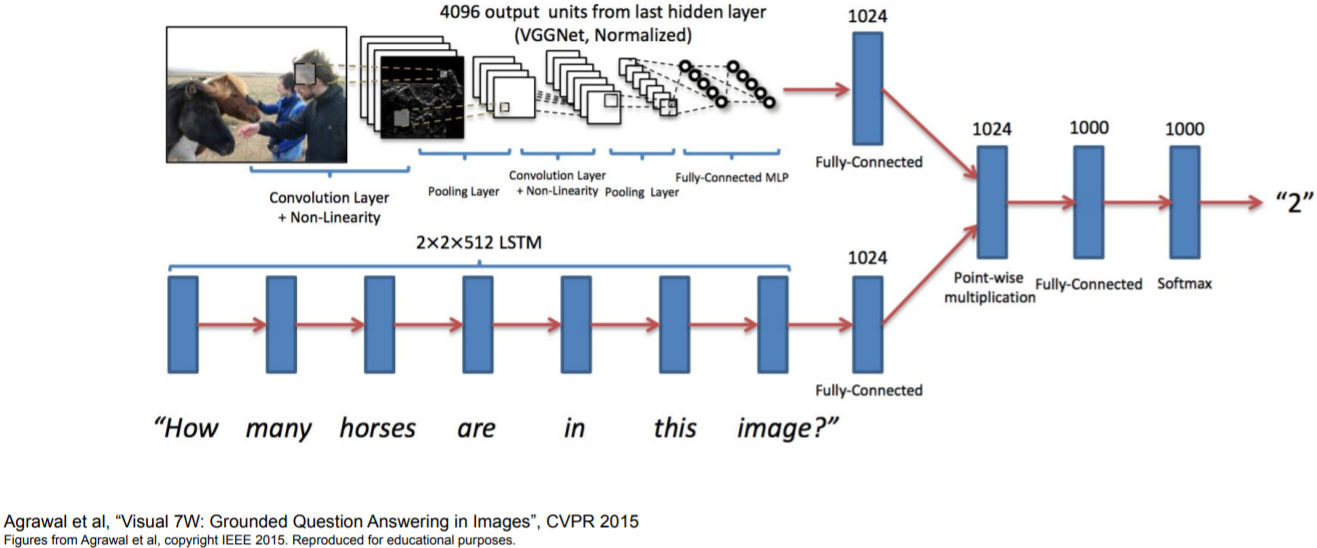
Image Captioning: CNN + RNN

• Instead of the final FC layer and the classifier in CNN, use FC output v(say 4096 length vector) to formulate the default hidden state $h_0$ in RNN.
  • before: $h = \mbox{tanh}(W_{xh}\ast x+W_{hh}\ast h)$
  • now: $h=\mbox{tanh}(W_{xh}\ast x + W_{hh}\ast h + W_{ih}\ast v)$
• RNN for Image Captioning
  Re-sample the previous output $y_{t-1}$ as the next input $x_t$, iterate untill $y_t$ sample takes <END> token.

Visual Question Answering: RNNs with Attention

Other tasks

• Visual Dialog: Conversations about images
• Visual Language Navigation: Go to the living room
  Agent encodes instructions in language and uses an RNN to generate a series of movements as the visual input changes after each move.
• Visual Question Answering: Dataset Bias
  With different types(Image + Question + Answer) of data used, model performances are better.

Long Short Term Memory (LSTM)

• Vanilla RNN
  \(h_t = \mbox{tanh}(W_{hh}h_{t-1} + W_{xh}x_t) \\ = \mbox{tanh}\left( (W_{hh} \ W_{hx}) {\begin{pmatrix} h_{t-1} \\ x_t \end{pmatrix}} \right) \\ = \mbox{tanh}\left( W {\begin{pmatrix} h_{t-1} \\ x_t \end{pmatrix}} \right)\)

• \(\frac{\partial h_t}{\partial h_{t-1}} = \mbox{tanh}' (W_{hh}h_{t-1} + W_{xh}x_t)W_{hh}\)
  $\frac{\partial L}{\partial W} = \sum_{t=1}^T \frac{\partial L_t}{\partial W}$

  \[\begin{align*} \frac{\partial L_T}{\partial W} &= \frac{\partial L_T}{\partial h_T} \frac{\partial h_t}{\partial h_{t-1}}\cdots \frac{\partial h_1}{\partial W} \\ &= \frac{\partial L_T}{\partial h_T}(\prod_{t=2}^T \frac{\partial h_t}{\partial h_{t-1}})\frac{\partial h_1}{\partial W} \\ &= \frac{\partial L_T}{\partial h_T}(\prod_{t=2}^T \mbox{tanh}'(W_{hh}h_{t-1} + W_{xh}x_t))W_{hh}^{T-1} \frac{\partial h_1}{\partial W} \end{align*}\]
• Problem
  As the output of tanh function are in range of [-1,1] and almost smaller than 1, vanilla RNN has vanishing gradients. If we assume no non-linearity, the gradient will be \(\frac{\partial L_T}{\partial W} = \frac{\partial L_T}{\partial h_T}W_{hh}^{T-1}\frac{\partial h_1}{\partial W}\). In this case, when the largest singular value is greater than 1, we have exploding gradients, while the value is smaller than 1, we have vanishing gradients.

H = 5	# dimensionality of hidden state
T = 50	# number of time steps
Whh = np.random.randn(H, H)

# forward pass of an RNN (ignoring inputs x)
hs = {}
ss = {}
hs[-1] = np.random.randn(H)
for t in xrange(T):
    ss[t] = np.dot(Whh, hs[t-1])
    hs[t] = np.maximum(0, ss[t])
	
# backward pass of the RNN
dhs = {}
dss = {}
dhs[T-1] = np.random.randn(H) #start off the chain with random gradient
for t in reversed(xrange(T)):
    dss[t] = (hs[t] > 0) * dhs[t]	# backprop through the nonlinearity
	dhs[t-1] = np.dot(Whh.T, dss[t])	# backprop into previous hidden state
		# "Whh.T" multiplied by "T" times!

• For exploding gradients: control with gradient clipping.
  For vanishing gradients: change the architecture, LSTM introduced.

• LSTM:
  \(\begin{pmatrix} i \\ f \\ o \\ g \end{pmatrix} = \begin{pmatrix} \sigma \\ \sigma \\ \sigma \\ \mbox{tanh}\end{pmatrix} W \begin{pmatrix} h_{t-1} \\ x_t \end{pmatrix}\)
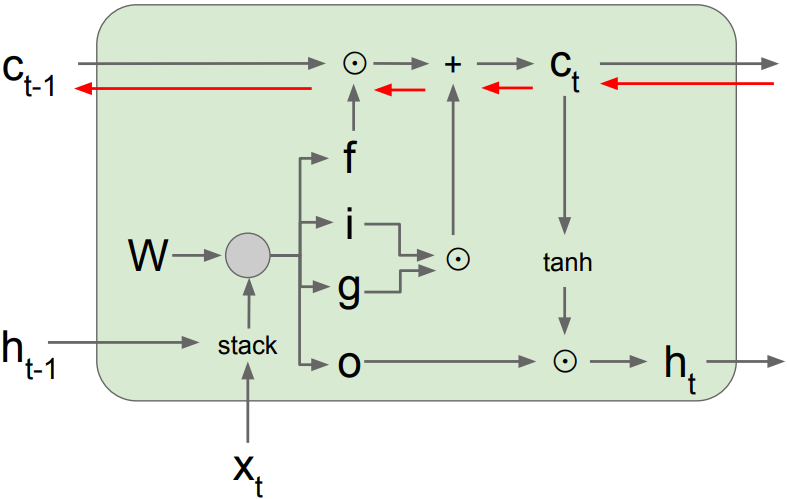
  \(c_t = f \odot c_{t-1} + i \odot g\), memory cell update
  \(h_t = o \odot \mbox{tanh}(c_t)\), hidden state update
  where W is a stack of $W_h$ and $W_x$

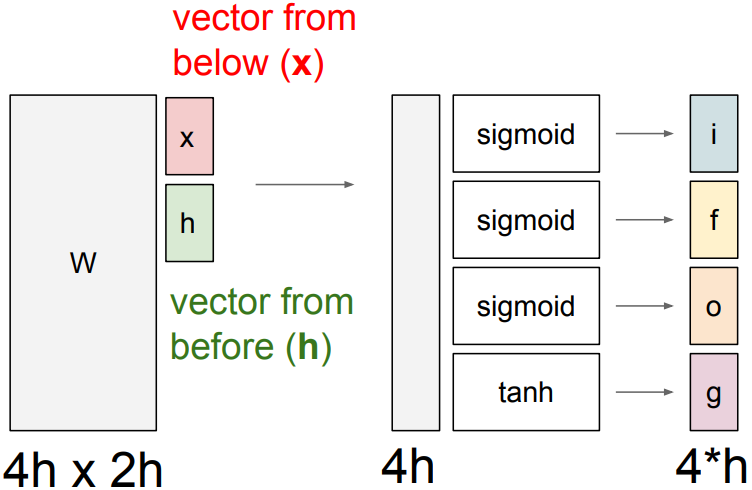
i: Input gate, whether to write to cell
f: Forget gate, Whether to erase cell
o: Output gate, How much to reveal cell
g: Gate gate, How much to write to cell

• Backpropagation from $c_t$ to $c_{t-1}$ only elementwise multiplication by f, no matrix multiply by W. Notice that the gradient contains the f gate’s vector of activations; it allows better control of gradients values, using suitable parameter updates of the forget gate. Also notice that are added through the f, i, g, and o gates, we can have better balancing of gradient values.

• Recall: “PlainNets” vs. ResNets
  ResNet is to PlainNet what LSTM is to RNN, kind of.
  Additive skip connections

• Do LSTMs solve the vanishing gradient problem?:
  The LSTM architecture makes it easier for the RNN to preserve information over many timesteps. e.g. If $f=1$ and $i=0$, then the information of that cell is preserved indefinitely. By contrast, it’s harder for vanilla RNN to learn a recurrent weight matrix $W_h$ that preserves information in hidden state.
  LSTM doesn’t guarantee that there is no vanishing/exploding gradient, but it does provide an easier way for the model to learn long-distance dependencies.

• in between: Highway Networks, Srivastava et al, 2015, [arXiv:1505.00387v2]
  A new architecture designed to ease gradient-based training of very deep networks. To regulate the flow of information and enlarge the possibility of studying extremely deep and efficient architectures.
  $g = T(x, W_T)$, $y = g \odot H(x, W_H) + (1-g)\odot x$

Other RNN Variants

• Neural Architecture Search(NAS) with Reinforcement Learning, Zoph et Le, 2017
  • RNN to design model; idea that we can represent the model architecture with a variable-length string.
  • Apply reinforcement learning on a neural network to maximize the accuracy(as a reward) on validation set, find a good architecture.
• GRU; smaller LSTM, “Learning phrase representations using rnn encoder-decoder for statistical machine translation”, Cho et al., 2014
• “An Empirical Exploration of Recurrent Network Architectures”, Jozefowicz et al., 2015
• LSTM: A Search Space Odyssey, Greff et al., 2015

Recurrence for Vision

• LSTM wer a good default choice until this year
• Use variants like GRU if you want faster compute and less parameters
• Use transformers (next lecture) as they are dominating NLP models
• almost everyday there is a new vision transformer model

Summary

• RNNs allow a lot of flexibility in architecture design
• Vanilla RNNs are simple but don’t work very well
• Common to use LSTM or GRU: their additive interactions improve gradient flow
• Backward flow of gradients in RNN can explode or vanish. Exploding is controlled with gradient clipping. Vanishing is controlled with additive interactions (LSTM)
• Better/simpler architectures are a hot topic of current research, as well as new paradigms for reasoning over sequences
• Better understanding (both theoretical and empirical) is needed.